Interpolation

Maple 2018 contains a new package for interpolating structured and unstructured data in any dimension. The supported methods include Kriging, inverse distance weighted, natural neighbor, and more. 

The Interpolate command provides an interface to all interpolation methods. It returns objects that behave like normal mathematical functions. 

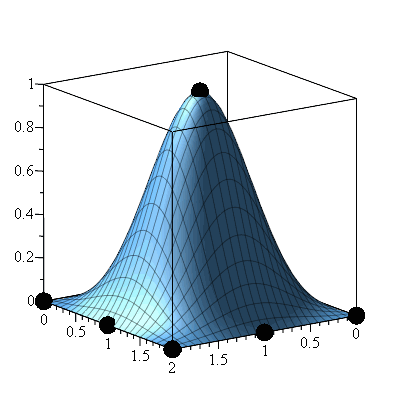Previous versions of Maple already included interpolation methods for 1-dimensional data and data given for a grid of points, like in the previous example. But Maple 2018 is the first version where you can interpolate data given for points in arbitrary, unstructured locations. 

The kriging interpolation method supports some extra functionality backed by statistical theory. In particular, it allows one to generate random data that is spatially correlated according to a so-called variogram. Here is an example: 

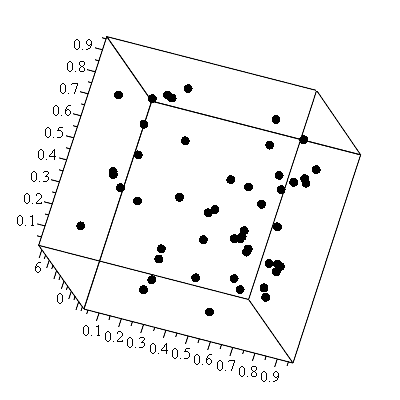We can now define an interpolating object using the Kriging method, and tell it the variogram used for its input. 

The interpolating object can return function values as if it were a regular mathematical function: 

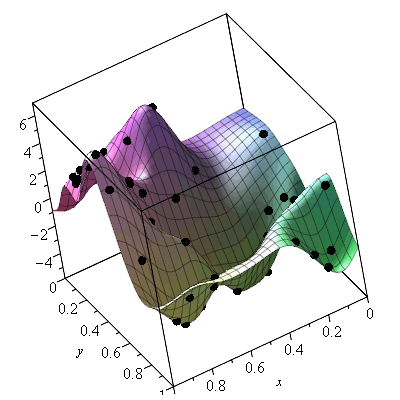It can also compute the variance associated with such function values - which gives a sense of the confidence in this value. 

We can visualize this variance by colouring the interpolated surface according to it. 

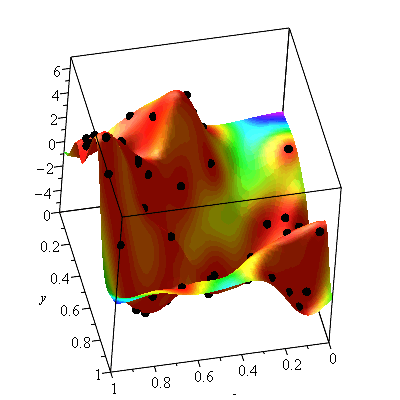In this visualization, red areas have high confidence and yellow, green, and blue areas have less confidence.