
The ThermophysicalData package
Additionally, the ScientificConstants has updated the non-derived physical constants to reflect those in the 2014 release of the CODATA Recommended Values of the Fundamental Physical Constants.
Maple 2018 introduces the Chemicals subpackage. This uses a new data source* to give the thermodynamic properties of over 2000 gases, liquids and crystalline species.
* Bonnie J. McBride, Michael J. Zehe, and Sanford Gordon. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species; 2002; https://www.grc.nasa.gov/WWW/CEAWeb/TP-2002-21556.htm .
The data can be used to study
| > |
Heat of formation and molar mass of gaseous CO2
| > |
Enthalpy and entropy of gaseous CO2 at 300 K
| > |
Liquid butane is burnt with 100% theoretical air at an initial temperature of 298.15 K. The combustion reaction is
C4H10 (l) + 6.5 O2 (g)+ 24.44 N2 (g) → 4 CO2 (g) + 5 H2O (g) + 24.44 N2 (g)
Here, we will calculate the adiabatic flame temperature of the combustion products.
Heat of formation of butane
| > |
Enthalpies of the combustion products at a temperature T
| > |
Enthalpy of the reactants
| > |
Total enthalpy of the combustion products
| > |
Equating the enthalpy of the reactants and the enthalpy of the combustion products gives the adiabatic flame temperature
| > |
One mole of CO and 0.5 moles of O2 are burned at 3000 K
CO (g) + 0.5 O2 (g) → CO2 (g)
The combustion products undergo dissociation and contain CO2, CO, O and O2. Here, we will calculate the equilibrium composition of the combustion products
Enthalpies as a function of temperature
| > |
Entropy as a function of temperature
| > |
Gibbs Free Energy as a function of temperature
| > |
Universal gas constant
| > |
Balancing the reactants and products gives
CO + 0.5 O2 = n1 CO2+ n2 CO + n3 O + n4 O2
This results in the following constraint on the oxygen atoms...
| > |
...and this constraint on the carbon atoms
| > |
Total number of moles in products
| > |
For a given temperature, minimizing the Gibbs Free Energy of the combustion products will give the equilibrium molar composition
| > | 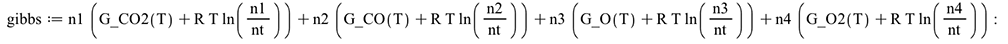 |
| > | 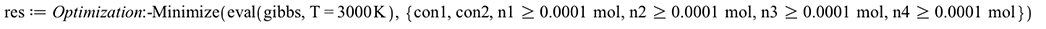 |
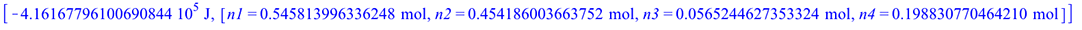 |
Maple 2018 updates the CoolProp library to version 6.1. This includes new fluids and updated routines used to calculate fluid properties.
New fluids include Dichloroethane, DiethylEther, EthyleneOxide, HydrogenChloride, Novec 649TM and several others
| > |
| > |
The non-derived physical constants in the ScientificConstants package now uses the most recent values of the scientific constants published by CODATA.
| > |
| > |