
Maple 2019 includes numerous cutting-edge updates in a variety of branches of mathematics.
Differential Equations
The new command FindODE, in the DEtools package, tries to find a linear ordinary differential equation with polynomial coefficients for the given expression.
| > |
| > |
int
Description
int Examples
| > |
| > |
| > | 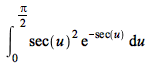 |
| > | 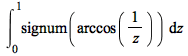 |
| > |
 |
| > | 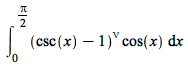 |
| > | 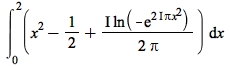 |
| > |
![Typesetting:-mprintslash([`+`(`*`(`/`(1, 2), `*`(PIECEWISE([`+`(`-`(`*`(`^`(ceil(`+`(x, `-`(`/`(1, 2)))), 2))), `*`(x, `*`(PIECEWISE([`+`(`*`(2, `*`(x)), `-`(1)), (`+`(x, `/`(1, 2)))::integer], [`+`(`...](AdvancedMath/AdvancedMath_20.gif) |
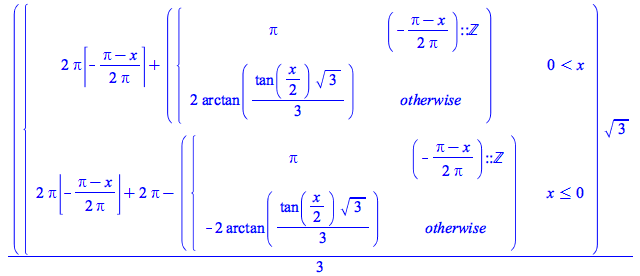
| > |
 |
| > |
![Typesetting:-mprintslash([PIECEWISE([`+`(`-`(`*`(`+`(I), `*`(Pi))), Ei(`+`(ln(`+`(`-`(x))), `*`(I, `*`(Pi))))), `<`(x, 0)], [0, x = 0], [Ei(ln(x)), `<`(x, 1)], [`+`(`-`(infinity)), x = 1], [Ei(ln(x)),...](AdvancedMath/AdvancedMath_24.gif) |
Integral Transforms
Description
Fourier Examples
| > | 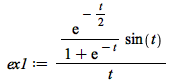 |
![Typesetting:-mprintslash([ex1 := `/`(`*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(t))))), `*`(sin(t))), `*`(`+`(1, exp(`+`(`-`(t)))), `*`(t)))], [`/`(`*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(t))))), `*`(sin(t))), `*`...](AdvancedMath/AdvancedMath_26.gif) |
| > |
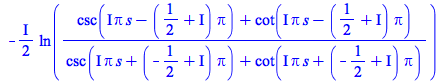 |
| > |
| > |
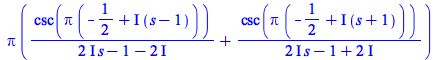 |
| > |
| > |
| > |
| > |
Multivariate Limits
The limit command in Maple 2019 has been enhanced for the case of limits of quotients of multivariate functions. See Multivariate Limits for details.
Real Roots of Polynomials
A new algorithm for univariate polynomials has been added to the RootFinding:-Isolate command. It is particularly efficient for ill-conditioned problems and high accuracy solutions, and it provides certified real root isolation for polynomials with irrational coefficients. See Real Root Finding for details.
Residue
The residue command has a new optional argument that allows the user to specify the maximal order of the underlying series computations.
simplify
Description
simplify Examples
Equal, equivalent, or implied piecewise branches are now combined by simplify;
| > | 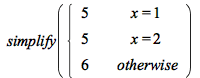 |
![Typesetting:-mprintslash([PIECEWISE([5, Or(x = 1, x = 2)], [6, otherwise])], [piecewise(Or(x = 1, x = 2), 5, 6)])](AdvancedMath/AdvancedMath_42.gif) |
| > | 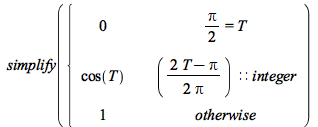 |
![Typesetting:-mprintslash([PIECEWISE([cos(T), (`+`(`-`(`/`(`*`(`/`(1, 2), `*`(`+`(`-`(`*`(2, `*`(T))), Pi))), `*`(Pi)))))::integer], [1, otherwise])], [piecewise((`+`(`-`(`/`(`*`(`/`(1, 2), `*`(`+`(`-`...](AdvancedMath/AdvancedMath_44.gif) |
| > | 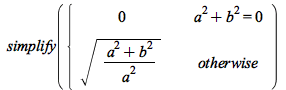 |
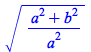 |
| > | ![`assuming`([simplify(piecewise(`<`(m, 2), floor(`+`(`*`(`/`(1, 2), `*`(m)))), 0))], [m::posint])](AdvancedMath/AdvancedMath_47.gif) |
Piecewise conditions involving floor, ceil, round, frac, trunc can now be simplified:
| > | 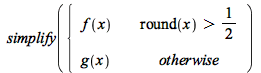 |
![Typesetting:-mprintslash([PIECEWISE([g(x), `<`(x, `/`(1, 2))], [f(x), `<=`(`/`(1, 2), x)])], [piecewise(`<`(x, `/`(1, 2)), g(x), `<=`(`/`(1, 2), x), f(x))])](AdvancedMath/AdvancedMath_50.gif) |
Branch conditions other than equations, inequations, and inequalities are now taken into account while simplifying branch values:
| > | 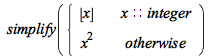 |
![Typesetting:-mprintslash([PIECEWISE([x, x::integer], [`*`(`^`(x, 2)), otherwise])], [piecewise(x::integer, x, `*`(`^`(x, 2)))])](AdvancedMath/AdvancedMath_52.gif) |
| > | 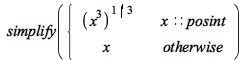 |
Branch conditions are now simplified more effectively using basic boolean logic:
| > | 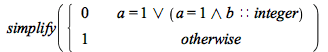 |
![Typesetting:-mprintslash([PIECEWISE([0, a = 1], [1, otherwise])], [piecewise(a = 1, 0, 1)])](AdvancedMath/AdvancedMath_56.gif) |
| > | 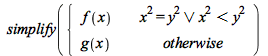 |
![Typesetting:-mprintslash([PIECEWISE([f(x), `<=`(`*`(`^`(x, 2)), `*`(`^`(y, 2)))], [g(x), otherwise])], [piecewise(`<=`(`*`(`^`(x, 2)), `*`(`^`(y, 2))), f(x), g(x))])](AdvancedMath/AdvancedMath_58.gif) |
simplify now reorders piecewise conditions when appropriate:
| > | 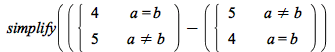 |
Piecewise conditions are now better normalized;
| > | 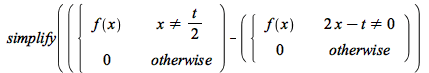 |
Common terms and factors are now pulled out of piecewise branch values where possible:
| > | 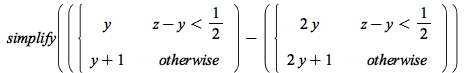 |
| > | ![simplify(piecewise(x = 0, `+`(`-`(`*`(4, `*`(Pi, `*`(_C8[_Z1, _Z2], `*`(`^`(BesselJ(_Z1, `*`(BesselJZeros(_Z1, _Z2), `*`(r))), 2), `*`(r))))))), `+`(`-`(`*`(2, `*`(Pi, `*`(_C8[_Z1, _Z2], `*`(`^`(Besse...](AdvancedMath/AdvancedMath_65.gif) |
![Typesetting:-mprintslash([`*`(PIECEWISE([-4, _Z1 = 0], [-2, otherwise]), `*`(Pi, `*`(_C8[_Z1, _Z2], `*`(`^`(BesselJ(_Z1, `*`(BesselJZeros(_Z1, _Z2), `*`(r))), 2), `*`(r)))))], [`*`(piecewise(_Z1 = 0, ...](AdvancedMath/AdvancedMath_66.gif) |
Improved simplification of ![]() :
:
| > |
Trig functions are now expanded if it helps with simplification:
| > |
Simplification of expressions containing arctan has been improved:
| > | 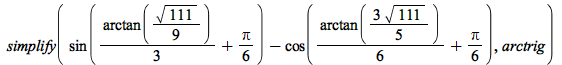 |
Expressions containing csgn can now be more effectively simplified:
| > |
Conversion between powers, exponentials, trig functions, and radicals to achieve simplification has been improved:
| > |
| > |
| > |
| > |
Symbolic powers of integers are now combined more effectively:
| > |
simplify now rewrites expressions using a common integer base:
| > |
Radicals are now typically combined by simplify:
| > |
If appropriate conditions are satisfied, certain simplifications of floor, ceil, and round are applied:
| > |
| > |
![]() now simplifies:
now simplifies:
| > |
solve
Description
solve Examples
Maple2019 solves equations with inequalities more carefully:
| > |
| > |
| > |
| > |
Other Improvements
Description
Other examples
minimize can now solve this example:
| > |
expand now takes into account more assumptions:
| > |
floor and ceil now make better use of assumptions:
| > |
rationalize works better on certain examples of nested radicals:
| > | 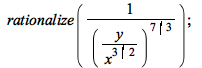 |
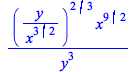 |
Expressions with nested calls to Re and Im now evaluate better:
| > |