
Overall, the enhancements throughout the entire package increase robustness, versatility and functionality, extending furthermore the range of Physics-related algebraic computations that can be done naturally in a worksheet. The presentation below illustrates both the novelties and the kind of mathematical formulations that can now be performed.
As part of its commitment to providing the best possible environment for algebraic computations in Physics, Maplesoft launched a Maple Physics: Research and Development website with Maple 18, which enabled users to download research versions, ask questions, and provide feedback. The results from this accelerated exchange with people around the world have been incorporated into the Physics package in Maple 2019.
Tensor product of Quantum States using Dirac's Bra-Ket Notation
Tensor products of Hilbert spaces and related quantum states are relevant in a myriad of situations in quantum mechanics, and in particular regarding quantum information. Tensor products are key in the mathematical formulation of entanglement. Below is a presentation of the design and implementation introduced in Maple 2019, with input/output and examples, organized in four sections:
References
[1] Cohen-Tannoudji, C.; Diu, B.; and Laloe,F. Quantum Mechanics, Chapter 2, section F.
[2] Griffiths, Robert B. Hilbert Space Quantum Mechanics. Quantum Computation and Quantum Information Theory Course, Physics Department, Carnegie Mellon University, 2014.
The basic ideas and design implemented in Maple 2019
Suppose ![]() and
and ![]() are quantum operators and
are quantum operators and ![]() are, respectively, their eigenkets. The following works since the introduction of the Physics package in Maple
are, respectively, their eigenkets. The following works since the introduction of the Physics package in Maple
| > |
| > |
| (1) |
| > |
| (2) |
| > |
| (3) |
In previous Maple releases, all quantum operators are supposed to act on the same Hilbert space. New in Maple 2019: suppose that ![]() and
and ![]() act on different, disjointed, Hilbert spaces.
act on different, disjointed, Hilbert spaces.
1) To represent that situation, a new keyword in Setup, ![]() , is introduced. With it you can indicate the quantum operators that act on a Hilbert space, say as in
, is introduced. With it you can indicate the quantum operators that act on a Hilbert space, say as in ![]() with the meaning that the operator
with the meaning that the operator ![]() acts on one Hilbert space while
acts on one Hilbert space while ![]() acts on another one.
acts on another one.
The Hilbert space thus has no particular name (as in 1, 2, 3 ...) and is instead identified by the operators that act on it. There can be one or more, and operators acting on one space can act on other spaces too. The disjointedspaces keyword is a synonym for hilbertspaces and hereafter all Hilbert spaces are assumed to be disjointed.
NOTE: noncommutative quantum operators acting on disjointed spaces commute between themselves, so after setting - for instance - ![]() , automatically,
, automatically, ![]() become quantum operators satisfying (see comment (ii) on page 156 of ref.[1])
become quantum operators satisfying (see comment (ii) on page 156 of ref.[1])
![]()
2) Product of Kets and Bras that belong to different Hilbert spaces are understood as tensor products satisfying (see footnote on page 154 of ref. [1]):
![]()
![]()
while
![]()
3) All the operators of one Hilbert space act transparently over operators, Bras, and Kets of other Hilbert spaces. For example
![]()
and the same for the Dagger of this equation, that is
![]()
Hence, when we write the left-hand sides of the two equations above and press enter, they are automatically rewritten (returned) as the right-hand sides.
4) Every other quantum operator, set as such using Setup, and not indicated as acting on any particular Hilbert space, is assumed to act on all spaces.
5) Notation:
![]()
is displayed as
![]()
Design details
The commutativity of the eigenkets of ![]() and
and ![]() is consistent with
is consistent with ![]() , see footnote on page 154 of ref. [1].
, see footnote on page 154 of ref. [1].
Taking advantage of this commutativity of Bras and Kets belonging to disjointed spaces, during the computer algebra session (on the worksheet) the ordering of their products in the output happens automatically and systematically, it is always the same, and according to the following rules: suppose there are two Hilbert subspaces, then:
Example: if one Hilbert subspace has operators ![]() acting on it and the other has operators
acting on it and the other has operators ![]() then a product of contiguous eigenkets of these operators is sorted as
then a product of contiguous eigenkets of these operators is sorted as
![]()
Where the first pair of Kets belong to the first Hilbert subspace and the other pair to the second subspace, and where the first subspace is the one whose operands are alphabetically sorted first than the operands of the second subspace (in this example ![]() is sorted before
is sorted before ![]() ) and within a subspace, the Kets are also sorted alphabetically (so
) and within a subspace, the Kets are also sorted alphabetically (so ![]() before
before ![]() , then in the second subspace
, then in the second subspace ![]() before
before ![]() ).
).
Regarding the notation for the Dagger of a tensor product of states, say ![]() the standard convention for tensor products is to preserve the order, as in
the standard convention for tensor products is to preserve the order, as in ![]() representing an exception to the “reverse the order†rule of the Dagger operation. This is conventional, in that Kets and Bras belonging to disjointed spaces actually commute. This convention, however is notationally important for two reasons
representing an exception to the “reverse the order†rule of the Dagger operation. This is conventional, in that Kets and Bras belonging to disjointed spaces actually commute. This convention, however is notationally important for two reasons
Example: we know that
![]()
In the left-hand and right-hand sides of the expression above, the ordering of the Hilbert subspaces is not the same. If we now omit the labels ![]() and
and ![]() , we would have
, we would have
![]()
which would be misleading. Likewise,
![]()
and removing the labels we would get the misleading
![]()
From all this we see that, in order to make sense of the notation without labels, it is necessary to preserve the ordering of the Hilbert subspaces present in a tensor product, and also when taking the Dagger of a Ket. Accordingly, within tensor products, for instance in these examples, the system will always write Kets of the subspace A before Kets of the subspace B.
Tensor product notation and the hideketlabel option
According to the design section, set now two disjointed Hilbert spaces with operators ![]() acting on one of them and
acting on one of them and ![]() on the other one (you can think of
on the other one (you can think of ![]() )
)
| > |
| (4) |
Consider a tensor product of Kets, each of which belongs to one of these different spaces, note the new notation using![]()
| > |
| (5) |
| > |
| (6) |
You see that in the product of Bras, and also in the product of Kets, A comes first, then B.
Remark: some textbooks prefer a dyadic style for sorting the operands in products of Bras and Kets that belong to different spaces, for example, ![]() instead of the projector sorting style of
instead of the projector sorting style of ![]() . Both reorderings of Kets and Bras are mathematically equal.
. Both reorderings of Kets and Bras are mathematically equal.
| > |
| (7) |
The display for ![]() is now
is now
| > |
| (8) |
Important: this new option only hides the label while displaying the Bra or Ket. The label, however, is still there, both in the input and in the output. One can "see" what is behind this new display using show, that works the same way as it does in the context of CompactDisplay. The actual contents being displayed in ![]() is thus
is thus ![]()
| > |
| (9) |
Operators of each of these spaces act on their eigenkets as usual. Here we distribute over both sides of an equation, using `*` on the left-hand side, to see the product uncomputed, and `.` on the right-hand side to see it computed:
| > |
| (10) |
| > |
| (11) |
| > |
| (12) |
| > |
| (13) |
Release the product
| > |
| (14) |
The same operation but now using the dot product `.` operator. Start by delaying the operation
| > |
| (15) |
Recalling that this product is mathematically the same as ![]() , and that
, and that
| > |
| (16) |
by releasing the delayed product ![]() we have
we have
| > |
| (17) |
Reset hideketlabel
| > |
| (18) |
Implementation details
| > |
| (19) |
| > |
| (20) |
| > |
| (21) |
| > |
| (22) |
| > |
| (23) |
| > |
| (24) |
| > |
| (25) |
These three Physics:-Library routines, are the ones used internally by the Physics package to make decisions.
| > |
| (26) |
| > |
| (27) |
| > |
| (28) |
Example
| > |
| (29) |
| > |
| (30) |
Remove now the evaluation delay and the ordering on the right-hand side is automatically rearranged as in the left-hand side.
| > |
| (31) |
The same using the dot operator `.`
| > |
| (32) |
| > |
| (33) |
NOTE: the dot product operator, `.`, is used to perform contractions or attachments in the space of quantum states. Therefore, in the case of tensor products, it returns using the star product operator `*`, in that there is no meaning for the contraction of tensors of different (disjointed) Hilbert spaces.
Regarding the product of a Bra and a Ket belonging to disjointed spaces, we also have, automatically,
| > |
| (34) |
| > |
| (35) |
So the left-hand side is rewritten as the right-hand side, and ![]() is not a "scalar product", but an operator in the tensor product of spaces, since
is not a "scalar product", but an operator in the tensor product of spaces, since ![]() and
and ![]() belong to different disjointed spaces.
belong to different disjointed spaces.
Enclose again the input with ' ' to delay its evaluation
| > |
| (36) |
Release the evaluation
| > |
| (37) |
In the output above we see that ![]() is not interpreted as contraction between an operator and Ket, but as the product of
is not interpreted as contraction between an operator and Ket, but as the product of ![]() acting on
acting on ![]() where
where ![]() is the identity (projector) onto the
is the identity (projector) onto the ![]() space. That is, an operator of one disjointed space acts transparently over a Bra or a Ket of a different disjointed space. The same happens with
space. That is, an operator of one disjointed space acts transparently over a Bra or a Ket of a different disjointed space. The same happens with ![]() just that, while
just that, while ![]() moves to the right, jumping over a Bra or Ket (see
moves to the right, jumping over a Bra or Ket (see ![]() ),
), ![]() moves to the left:
moves to the left:
| > |
| (38) |
| > |
| (39) |
NOTE: Although determining "who is the Dagger of who" is arbitrary, this implementation follows what we do with paper and pencil: operators act to their right while those having an explicit Dagger act to their left.
Finally, the notation used for tensor products of operators is the same one used for tensor products of Bras and Kets:
| > |
| (40) |
As explained in the Details of the design section, the ordering of the Hilbert spaces in tensor products is now preserved, so taking the Dagger does not swap the operands in this product:
| > |
| (41) |
Entangled States and the Bell basis
With the introduction of disjointed Hilbert spaces in Maple 2019 it is possible to represent entangled quantum states in a simple way, basically as done with paper and pencil.
Recalling the Hilbert spaces set at this point are,
| > |
| (42) |
where ![]() acts on the tensor product of the spaces where
acts on the tensor product of the spaces where ![]() and
and ![]() act. A state of
act. A state of ![]() can then always be written as
can then always be written as
| > |
| (43) |
where ![]() is a matrix of complex coefficients. Bra states of
is a matrix of complex coefficients. Bra states of ![]() are formed as usual taking the Dagger
are formed as usual taking the Dagger
| > |
| (44) |
Example: the Bell basis for a system of two qubits
Consider a 2-dimensional space of states acted upon by the operator ![]() , and let
, and let ![]() act upon another, disjointed, Hilbert space that is a replica of the Hilbert space on which
act upon another, disjointed, Hilbert space that is a replica of the Hilbert space on which ![]() acts. Set the dimensions of
acts. Set the dimensions of ![]() ,
, ![]() and
and ![]() respectively equal to 2, 2 and 2x2
respectively equal to 2, 2 and 2x2
| > |
| (45) |
The system C with the two subsystems A and B represents a two qubits system. The standard basis for C can be constructed in a natural way from the basis of Kets of A and B, ![]() , by taking their tensor products:
, by taking their tensor products:
| > |
| (46) |
Set a more mathematical display for the imaginary unit
| > |
The four entangled Bell states also form a basis of C and are given by
| > |
| (47) |
| > |
| (48) |
| > |
| (49) |
| > |
| (50) |
| > |
| (51) |
There is no standard convention for the four linear combinations of the right-hand sides above defining the Bell states. The convention used here relates to the definition of these states using the Pauli matrices as shown further below. Regardless of the convention used, the Bell basis is orthonormal. That can be verified by taking dot products, for example:
| > |
| (52) |
In steps, perform the same operation but using the star (`*`) operator, so that the contraction is represented but not performed
| > |
| (53) |
Evaluate now the result at `*` = `.`, that is transforming the star product into a dot product
| > |
| (54) |
| > |
| (55) |
| > |
| (56) |
The Bell basis and its relation with the Pauli matrices
The Bell basis can be constructed departing from ![]() using the Pauli matrices
using the Pauli matrices ![]() . For that purpose, using a Vector representation for
. For that purpose, using a Vector representation for ![]() ,
,
| > |
 |
(57) |
Multiplying ![]() by each of the
by each of the ![]() Pauli matrices and performing the matrix operations we have
Pauli matrices and performing the matrix operations we have
| > |
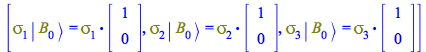 |
(58) |
| > |
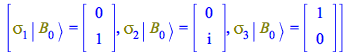 |
(59) |
In this result we see that ![]() and
and ![]() flip the state, transforming
flip the state, transforming ![]() into
into ![]() ,
, ![]() also multiplies by the imaginary unit
also multiplies by the imaginary unit ![]() , while
, while ![]() leaves the state
leaves the state ![]() unchanged.
unchanged.
We can express all that by removing from ![]() the Vector representations shown in
the Vector representations shown in ![]() . For that purpose, create a list of substitution equations
. For that purpose, create a list of substitution equations
| > |
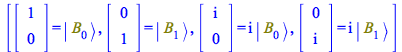 |
(60) |
The action of ![]() in
in ![]() is then given by
is then given by
| > |
| (61) |
For ![]() , performing the same steps, the action of the Pauli matrices on it is
, performing the same steps, the action of the Pauli matrices on it is
| > |
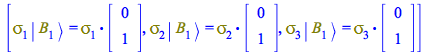 |
(62) |
| > |
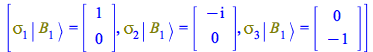 |
(63) |
| > |
| (64) |
To obtain the other three Bell states using the results ![]() and
and ![]() , indicate to the system that the Pauli matrices operate in the subspace where
, indicate to the system that the Pauli matrices operate in the subspace where ![]() operates
operates
| > |
| (65) |
Multiplying ![]() given in
given in ![]() by each of the three
by each of the three ![]() we get the other three Bell states
we get the other three Bell states
| > |
| (66) |
| > |
| (67) |
Substitute in this result the first equations of ![]() and
and ![]()
| > |
| (68) |
| > |
| (69) |
| > |
| (70) |
| > |
| (71) |
This is ![]() defined in
defined in ![]()
| > |
| (72) |
| > |
| (73) |
Multiplying now by ![]() and substituting
and substituting ![]() using the
using the ![]() equations of
equations of ![]() and
and ![]() we get
we get ![]()
| > |
| (74) |
| > |
| (75) |
| > |
| (76) |
| > |
| (77) |
The above is ![]() defined in
defined in ![]()
| > |
| (78) |
| > |
| (79) |
Finally, multiplying ![]() by
by ![]()
| > |
| (80) |
Substituting
| > |
| (81) |
| > |
| (82) |
We get
| > |
| (83) |
which is ![]()
| > |
| (84) |
| > |
| (85) |
Reset the symbol representing imaginary unit to use i as an index in the next section
| > |
Entangled States, Operators and Projectors
Consider a fourth operator, ![]() , that is Hermitian and acts on the same space of
, that is Hermitian and acts on the same space of ![]() , has the same dimension, and
, has the same dimension, and ![]() are its mean values in an entangled and product states respectively.
are its mean values in an entangled and product states respectively.
| > |
| (86) |
To operate in a practical way with these operators, Bras and Kets, bracket rules reflecting their relationship are necessary. From the definition of ![]() as acting on the tensor product of spaces where
as acting on the tensor product of spaces where ![]() and
and ![]() act (see
act (see ![]() ) and taking into account the dimensions specified for
) and taking into account the dimensions specified for ![]() ,
, ![]() and
and ![]() we have
we have
| > |
![Typesetting:-mprintslash([Physics:-Ket(C, a, b) = Sum(Sum(`*`(M[a, j, b, p], `*`(Physics:-`*`(Physics:-Ket(A, j), Physics:-Ket(B, p)))), j = 0 .. 1), p = 0 .. 1)], [Physics:-Ket(C, a, b) = Sum(Sum(`*`...](Physics/Physics_347.gif) |
(87) |
| > |
![Typesetting:-mprintslash([Physics:-Bracket(Physics:-Bra(A, k), Physics:-Ket(C, a, b)) = Sum(`*`(M[a, k, b, p], `*`(Physics:-Ket(B, p))), p = 0 .. 1)], [Physics:-Bracket(Physics:-Bra(A, k), Physics:-Ke...](Physics/Physics_349.gif) |
(88) |
| > |
![Typesetting:-mprintslash([Physics:-Bracket(Physics:-Bra(B, k), Physics:-Ket(C, a, b)) = Sum(`*`(M[a, j, b, k], `*`(Physics:-Ket(A, j))), j = 0 .. 1)], [Physics:-Bracket(Physics:-Bra(B, k), Physics:-Ke...](Physics/Physics_351.gif) |
(89) |
| > |
| (90) |
The bracket rules for ![]() ,
, ![]() and
and ![]() are the first two of these; Set these rules, so that the system can take them into account
are the first two of these; Set these rules, so that the system can take them into account
| > |
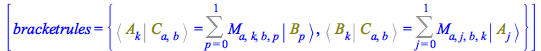 |
(91) |
If we now recompute ![]() , the left-hand side is also computed
, the left-hand side is also computed
| > |
| (92) |
Suppose now that you want to compute with the Hermitian operator ![]() , that operates on the same space as
, that operates on the same space as ![]() , both using C and the operators
, both using C and the operators ![]() and
and ![]() , as in
, as in
![]()
![]()
where ![]() =
= ![]() when
when ![]() is a product (not entangled) state.
is a product (not entangled) state.
To compute taking into account ![]() it suffices to set a bracket rule
it suffices to set a bracket rule
| > |
| (93) |
After that,
| > |
| (94) |
Regarding ![]() , since
, since ![]() belongs to the tensor product of spaces A and B, it can be an entangled operator, one that you cannot represent just as a product of one operator acting on A times another one acting on B. A computational representation for the operator
belongs to the tensor product of spaces A and B, it can be an entangled operator, one that you cannot represent just as a product of one operator acting on A times another one acting on B. A computational representation for the operator ![]() (that is not just itself or as abstract) is not possible in the general case. For that you can use a different feature: define the action of the operator
(that is not just itself or as abstract) is not possible in the general case. For that you can use a different feature: define the action of the operator ![]() on Kets of
on Kets of ![]() and
and ![]() .
.
Basically, we want:
![]()
![]()
![]()
A program sketch for that would be:
if H is applied to a Ket of A or B and it still has not 4 indices then
if H itself is indexed then
return H with its indices followed by the index of the Ket
else
return H indexed by the index of the Ket;
otherwise
return the dot product operation uncomputed, unevaluated
In the Maple language (see sec. 1.4) that program-sketch becomes
| > |
Let's see it in action. Start by erasing the Physics performance remember tables, which remember results like computed before the definition of ![]()
| > |
| > |
| (95) |
Recalling that ![]() is Hermitian,
is Hermitian,
| > |
| (96) |
| > |
| (97) |
| > |
| (98) |
| > |
| (99) |
Note that the definition of ![]() as a procedure does not interfere with the setting of an bracket rule for it with
as a procedure does not interfere with the setting of an bracket rule for it with ![]() , that is still working
, that is still working
| > |
| (100) |
where â„‹ = â„ when ![]() is a product state. The definition of H takes precedence, so if in that definition you indicate what to do with a
is a product state. The definition of H takes precedence, so if in that definition you indicate what to do with a ![]() Ket, that will be taken into account before the bracket rule.
Ket, that will be taken into account before the bracket rule.
| > |
![Typesetting:-mprintslash([`𝕀__A` := Sum(Physics:-`*`(Physics:-Ket(A, i), Physics:-Bra(A, i)), i = 0 .. 1)], [Sum(Physics:-`*`(Physics:-Ket(A, i), Physics:-Bra(A, i)), i = 0 .. 1)])](Physics/Physics_422.gif) |
|
![Typesetting:-mprintslash([`𝕀__B` := Sum(Physics:-`*`(Physics:-Ket(B, i), Physics:-Bra(B, i)), i = 0 .. 1)], [Sum(Physics:-`*`(Physics:-Ket(B, i), Physics:-Bra(B, i)), i = 0 .. 1)])](Physics/Physics_423.gif) |
|
![Typesetting:-mprintslash([`𝕀__C` := Sum(Sum(Physics:-`*`(Physics:-Ket(C, a, b), Physics:-Bra(C, a, b)), a = 0 .. 1), b = 0 .. 1)], [Sum(Sum(Physics:-`*`(Physics:-Ket(C, a, b), Physics:-Bra(C, a, ...](Physics/Physics_424.gif) |
(101) |
Since the algebra rules for computing with eigenkets of ![]() ,
, ![]() and
and ![]() were already set in
were already set in ![]() , from the projectors above you can construct any subspace projector, for example
, from the projectors above you can construct any subspace projector, for example
| > |
![Typesetting:-mprintslash([Sum(Sum(Sum(`*`(M[a, m, b, p], `*`(Physics:-`*`(Physics:-Ket(B, p), Physics:-Bra(C, a, b)))), p = 0 .. 1), a = 0 .. 1), b = 0 .. 1)], [Sum(Sum(Sum(`*`(M[a, m, b, p], `*`(Phys...](Physics/Physics_430.gif) |
(102) |
| > |
![Typesetting:-mprintslash([Sum(Sum(Sum(`*`(conjugate(M[a, m, b, p]), `*`(Physics:-`*`(Physics:-Ket(C, a, b), Physics:-Bra(B, p)))), p = 0 .. 1), a = 0 .. 1), b = 0 .. 1)], [Sum(Sum(Sum(`*`(conjugate(M[...](Physics/Physics_432.gif) |
(103) |
The conjugate of ![]() is due to the contraction or attachment from the right of
is due to the contraction or attachment from the right of ![]() , that is with
, that is with
| > |
![Typesetting:-mprintslash([Physics:-Bra(C, a, b) = Sum(Sum(`*`(conjugate(M[a, j, b, p]), `*`(Physics:-`*`(Physics:-Bra(A, j), Physics:-Bra(B, p)))), j = 0 .. 1), p = 0 .. 1)], [Physics:-Bra(C, a, b) = ...](Physics/Physics_436.gif) |
(104) |
The coefficients ![]() satisfy constraints due to the normalization of Kets of
satisfy constraints due to the normalization of Kets of ![]() and
and ![]() . One can derive these constraints by inserting the unit operator
. One can derive these constraints by inserting the unit operator ![]() in the identity
in the identity
| > |
![Sum(Sum(`*`(conjugate(M[a, r, b, s]), `*`(M[a, m, b, n])), a = 0 .. 1), b = 0 .. 1) = `*`(Physics:-KroneckerDelta[m, r], `*`(Physics:-KroneckerDelta[n, s]))](Physics/Physics_442.gif) |
(105) |
Transform this result into a function P to explore the identity further
| > |
![Typesetting:-mprintslash([P := proc (m, n, r, s) options operator, arrow; sum(sum(`*`(conjugate(M[a, r, b, s]), `*`(M[a, m, b, n])), a = 0 .. 1), b = 0 .. 1) = `*`(Physics:-KroneckerDelta[m, r], `*`(P...](Physics/Physics_444.gif) |
(106) |
The first and third indices refer to the quantum numbers of ![]() , the second and fourth to
, the second and fourth to ![]() , so the right-hand sides in the following are respectively 1 and 0
, so the right-hand sides in the following are respectively 1 and 0
| > |
| (107) |
| > |
| (108) |
To get the whole system of equations satisfied by the coefficients ![]() , use P to construct an Array with four indices running from 0..1
, use P to construct an Array with four indices running from 0..1
| > |
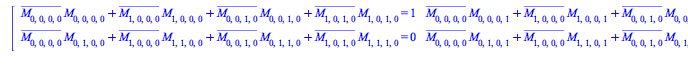 |
(109) |
Convert the whole Array into a set of equations
| > |
| (110) |
Coherent States in Quantum Mechanics
References
[1] Cohen-Tannoudji, C.; Diu, B.; and Laloe, F. Quantum Mechanics. Paris, France: Hermann, 1977.
[2] Massachusetts Institute of Technology OpenCourseWare, Quantum Physics II, Quantum Dynamics.
Definition and the basics
| > |
Set a quantum operator ![]() and corresponding annihilation / creation operators
and corresponding annihilation / creation operators
| > |
| (111) |
| > |
| (112) |
| > |
| (113) |
In what follows, on the left-hand sides the product operator used is `*`, which properly represents, but does not perform the attachment of Bras, Kets, and operators. On the right-hand sides the product operator is `.`, that performs the attachments. Since the introduction of Physics in the Maple system, we have that
| > |
| (114) |
| > |
| (115) |
| > |
| (116) |
New in Maple 2019: coherent states, the eigenstates of the annihilation operator ![]() , with all of their properties, are now understood as such by the system
, with all of their properties, are now understood as such by the system
| > |
| (117) |
![]() is an eigenket of
is an eigenket of ![]() but not of
but not of ![]()
| > |
| (118) |
The norm of these states is equal to 1
| > |
| (119) |
These states, however, are not orthonormal as the occupation number states ![]() are, and since
are, and since ![]() is not Hermitian, its eigenvalues are not real but complex numbers. Instead of
is not Hermitian, its eigenvalues are not real but complex numbers. Instead of ![]() , in Maple 2019 we have
, in Maple 2019 we have
| > |
| (120) |
At ![]() ,
,
| > |
| (121) |
Their scalar product with the occupation number states ![]() , using the inert %Bracket on the left-hand side and the active Bracket on the other side:
, using the inert %Bracket on the left-hand side and the active Bracket on the other side:
| > |
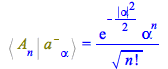 |
(122) |
The expansion of coherent states into occupation number states, first representing the product operation using `*`, then performing the attachments replacing `*` by `.`
| > |
| (123) |
| > |
| (124) |
| > |
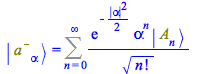 |
(125) |
Taking all into account,
| > |
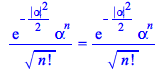 |
(126) |
Hide now the ket label. When in doubt, input show to see the Kets with their labels explicitly shown
| > |
| (127) |
Define eigenkets of the annihilation operator, with two different eigenvalues for experimentation
| > |
| (128) |
| > |
| (129) |
Because the properties of coherent states are now known to the system, the following computations proceed automatically in Maple 2019. The left-hand sides use the `*`, while the right-hand sides use the `.`
| > |
| (130) |
| > |
| (131) |
| > |
| (132) |
| > |
| (133) |
Properties of Coherent states
The mean value of the occupation number N
The occupation number operator N is given by
| > |
| (134) |
![]()
| > |
| (135) |
| > |
| (136) |
N is diagonal in the ![]() basis of the Fock (occupation number) space
basis of the Fock (occupation number) space
| > |
| (137) |
| > |
| (138) |
| > |
| (139) |
The mean value of ![]()
| > |
| (140) |
| > |
| (141) |
The standard deviation ![]() for a state
for a state ![]()
| > |
| (142) |
In conclusion, a coherent state ![]() has a finite spreading
has a finite spreading ![]() . Coherent states are good approximations for the states of a laser, where the laser intensity I is proportional to the mean value of the photon number, I âˆ
. Coherent states are good approximations for the states of a laser, where the laser intensity I is proportional to the mean value of the photon number, I ∠![]() , and so the intensity fluctuation,
, and so the intensity fluctuation, ![]() .
.
| > |
| (143) |
| > |
| (144) |
The mean value of the occupation number N in a state ![]() is thus n itself, as expected since
is thus n itself, as expected since ![]() represents a (Fock space) state of n (quasi-) particles. Accordingly,
represents a (Fock space) state of n (quasi-) particles. Accordingly,
| > |
| (145) |
| > |
| (146) |
The standard deviation ![]() for a state
for a state ![]() , is thus
, is thus
| > |
| (147) |
That is, in a Fock state, ![]() , there is no intensity fluctuation.
, there is no intensity fluctuation.
![]()
The specific properties of coherent states implemented in Maple 2019 can be derived explicitly departing from the projection of ![]() into the
into the ![]() basis of occupation number states and the definition of
basis of occupation number states and the definition of ![]() as the operator that annihilates the vacuum
as the operator that annihilates the vacuum ![]()
![]()
| > |
| (148) |
| > |
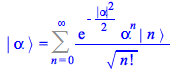 |
(149) |
To derive ![]() from the formula above, start multiplying by
from the formula above, start multiplying by ![]()
| > |
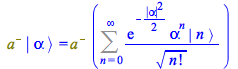 |
(150) |
In view of ![]() , discard the first term of the sum
, discard the first term of the sum
| > |
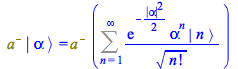 |
(151) |
Change variables ![]() ; in the result rename
; in the result rename ![]()
| > |
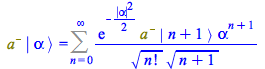 |
(152) |
Activate the product ![]() by replacing, in the right-hand side, the product operator `*` by `.`
by replacing, in the right-hand side, the product operator `*` by `.`
| > |
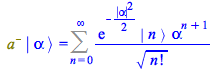 |
(153) |
By inspection the right-hand side of ![]() is equal to
is equal to ![]() times the right-hand side of
times the right-hand side of ![]()
| > |
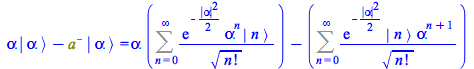 |
(154) |
| > |
| (155) |
Consider the projection of ![]() over an occupation number state
over an occupation number state ![]()
| > |
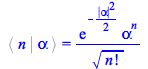 |
(156) |
An overview of the distribution of coherent states ![]() for a sample of values of n and
for a sample of values of n and ![]() is thus as follows
is thus as follows
| > |
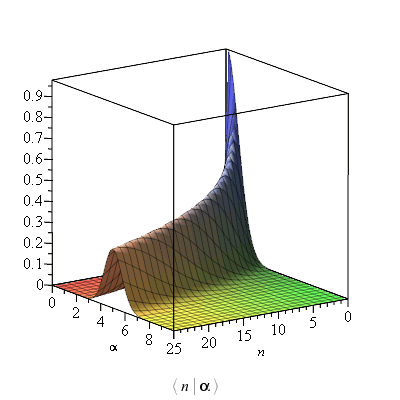 |
The distribution can be explored for ranges of values of n and ![]() using Explore
using Explore
| > |
| > |
|
||||||
|
||||||
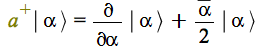
To verify this identity, construct each of the three terms, then simplify the result. Recalling the projection of a coherent state![]() into the
into the ![]() basis of occupation number states,
basis of occupation number states,
| > |
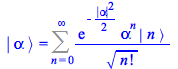 |
(157) |
The third term of this identity is thus
| > |
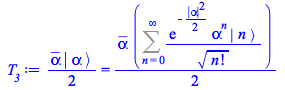 |
(158) |
The first term, on the left-hand side, is obtained multiplying by ![]()
| > |
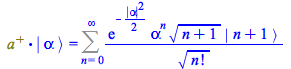 |
(159) |
To have the three terms with ![]() in the summand, change variables
in the summand, change variables ![]() ; in the result rename
; in the result rename ![]()
| > |
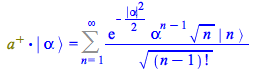 |
(160) |
The radical in the summand can be rewritten taking into account that, when n is a positive integer,
| > |
| (161) |
This identity can be verified as follows
| > |
| (162) |
| > |
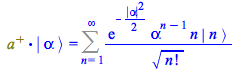 |
(163) |
The summand, at ![]() , is equal to 0
, is equal to 0
| > |
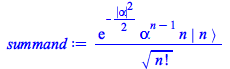 |
(164) |
| > |
| (165) |
Rewriting then the sum to start from 0
| > |
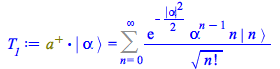 |
(166) |
The second term of this identity is obtained by differentiation of ![]()
| > |
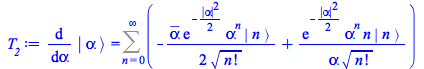 |
(167) |
Putting the three terms together,
| > |
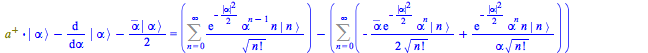  |
(168) |
Combining the sums the identity is verified
| > |
| (169) |
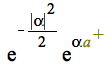
![]() =
= ![]()
The coherent state ![]() can be constructed from the vacuum state using the operator
can be constructed from the vacuum state using the operator ![]() .
.
| > |
| (170) |
| > |
![`𝒟`[1] = `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2)))))), `*`(exp(`*`(alpha, `*`(`#msup(mi(](Physics/Physics_658.gif) |
(171) |
New in Maple 2019, the conversion network for mathematical functions can be used with not-commutative variables; develop the exponential function of ![]() in power series:
in power series:
| > |
| (172) |
So ![]() becomes
becomes
| > |
![`𝒟`[1] = `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2)))))), `*`(Sum(`/`(`*`(Physics:-`^`(`*`(alpha, `*`(`#msup(mi(](Physics/Physics_664.gif) |
(173) |
Therefore, for ![]() ·
·![]() , we have
, we have
| > |
![Typesetting:-mprintslash([Physics:-`.`(`𝒟`[1], Physics:-Ket(A, 0)) = Sum(`/`(`*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2)))))), `*`(Physics:-`.`(Physics:-`^`(`*`(alpha, `*`(`#msup(mi(](Physics/Physics_668.gif) |
(174) |
| > |
![Typesetting:-mprintslash([Physics:-`.`(`𝒟`[1], Physics:-Ket(A, 0)) = Sum(`/`(`*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2)))))), `*`(`^`(alpha, n), `*`(Physics:-Ket(A, n)))), `*`(`^`(fact...](Physics/Physics_670.gif) |
(175) |
By inspection the right-hand side is already the projection of ![]() into the basis or occupation number states
into the basis or occupation number states ![]() computed previously in
computed previously in ![]()
| > |
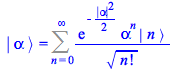 |
(176) |
| > |
| (177) |
| > |
| (178) |
Remark: ![]() is not unitary,
is not unitary, ![]()
| > |
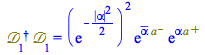 |
(179) |
| > |
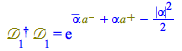 |
(180) |
![]()
![]() =
= ![]()
Here, we use another operator, ![]() =
= ![]() to construct
to construct ![]() from the vacuum.
from the vacuum. ![]() is sometime called the "displacement" operator. It has the advantage over
is sometime called the "displacement" operator. It has the advantage over ![]() that
that ![]() is unitary,
is unitary,![]() As a consequence:
As a consequence: ![]() .
.
| > |
| (181) |
This operator is unitary
| > |
| (182) |
| > |
| (183) |
To verify that ![]() one can proceed as in the above, or directly compute their commutator, expecting
one can proceed as in the above, or directly compute their commutator, expecting ![]() .
.
| > |
| (184) |
| > |
| (185) |
For ![]() ·
·![]() , start multiplying by
, start multiplying by ![]()
| > |
| (186) |
| > |
![Typesetting:-mprintslash([Physics:-`*`(`𝒟`[2], Physics:-Ket(A, 0)) = `*`(Physics:-`*`(exp(`*`(alpha, `*`(`#msup(mi(](Physics/Physics_715.gif) |
(187) |
Recalling the definition of ![]() in the previous section
in the previous section
| > |
![`𝒟`[1] = `*`(exp(`+`(`-`(`*`(`/`(1, 2), `*`(`^`(abs(alpha), 2)))))), `*`(exp(`*`(alpha, `*`(`#msup(mi(](Physics/Physics_718.gif) |
(188) |
The expression above ![]() can be simplified using this definition
can be simplified using this definition
| > |
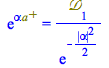 |
(189) |
| > |
| (190) |
In turn ![]() can be computed by replacing the `*` product by a dot product `.`
can be computed by replacing the `*` product by a dot product `.`
| > |
| (191) |
Finally, we arrive at the desired result recalling the result of the previous section,
| > |
| (192) |
| > |
| (193) |
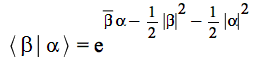
The identity in the title can be derived departing again from the projection of a coherent state![]() into the
into the ![]() basis of occupation number states
basis of occupation number states
| > |
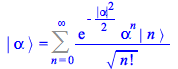 |
(194) |
| > |
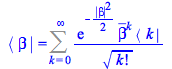 |
(195) |
Taking the `*` product of these two expressions
| > |
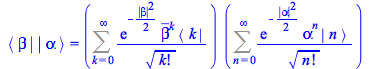 |
(196) |
Perform the attachment of Bras and Kets on the right-hand side by replacing `*` by `.`, evaluating the sum and simplifying the result
| > |
| (197) |
In most cases, ![]() and
and ![]() are complex valued numbers. Below, the plots assume that
are complex valued numbers. Below, the plots assume that ![]() and
and ![]() are both real. To take into account the general case, the possibility to tune a phase difference
are both real. To take into account the general case, the possibility to tune a phase difference ![]() between
between ![]() and
and ![]() is explicitly added, so that
is explicitly added, so that ![]() becomes
becomes
| > |
| (198) |
| > |
|
||||||
|
||||||
The Zassenhaus formula and the algebra of the Pauli matrices
The implementation of the Pauli matrices and their algebra were reviewed for Maple 2019, including the algebraic manipulation of nested commutators, resulting in faster computations using simpler and more flexible input. As it frequently happens, improvements of this type suddenly transform research problems presented in the literature as untractable in practice, into tractable.
As an illustration, we tackle below the derivation of the coefficients entering the Zassenhaus formula shown in section 4 of [1] for the Pauli matrices up to order 10 (results in the literature go up to order 5). The computation presented can be reused to compute these coefficients up to any desired higher-order (hardware limitations may apply). A number of examples which exploit this formula and its dual, the Baker-Campbell-Hausdorff formula, occur in connection with the Weyl prescription for converting a classical function to a quantum operator (see sec. 5 of [1]), as well as when solving the eigenvalue problem for classes of mathematical-physics partial differential equations [2].
References
Formulation of the problem
The Zassenhaus formula expresses ![]() as an infinite product of exponential operators involving nested commutators of increasing complexity
as an infinite product of exponential operators involving nested commutators of increasing complexity
![]()
![]()
Given ![]() ,
, ![]() and their commutator
and their commutator ![]() , if
, if ![]() and
and ![]() commute with
commute with ![]() ,
, ![]() for
for ![]() and the Zassenhaus formula reduces to the product of the first three exponentials above. The interest here is in the general case, when
and the Zassenhaus formula reduces to the product of the first three exponentials above. The interest here is in the general case, when ![]() and
and ![]() , and the goal is to compute the Zassenhaus coefficients
, and the goal is to compute the Zassenhaus coefficients ![]() in terms of
in terms of ![]() ,
, ![]() for arbitrary n. Following [1], in that general case, differentiating the Zassenhaus formula with respect to
for arbitrary n. Following [1], in that general case, differentiating the Zassenhaus formula with respect to ![]() and multiplying from the right by
and multiplying from the right by ![]() one obtains
one obtains
![]()
This is an intricate formula, which however (see eq.(4.20) of [1]) can be represented in abstract form as
![]()
from where an equation to be solved for each ![]() is obtained by equating to 0 the coefficient of
is obtained by equating to 0 the coefficient of ![]() . In this formula, the repeated commutator bracket is defined inductively in terms of the standard commutator
. In this formula, the repeated commutator bracket is defined inductively in terms of the standard commutator ![]() by
by
![]()
![]()
and higher-order repeated-commutator brackets are similarly defined. For example, taking the coefficient of ![]() and
and ![]() and respectively solving each of them for
and respectively solving each of them for ![]() and
and ![]() one obtains
one obtains
![]()
![]()
This method is used in [3] to treat quantum deviations from the classical limit of the partition function for both a Bose-Einstein and Fermi-Dirac gas. The complexity of the computation of ![]() grows rapidly and in the literature only the coefficients up to
grows rapidly and in the literature only the coefficients up to ![]() have been published. Taking advantage of developments in the Physics package for Maple 2019, below we show the computation up to
have been published. Taking advantage of developments in the Physics package for Maple 2019, below we show the computation up to ![]() and provide a compact approach to compute them up to arbitrary order.
and provide a compact approach to compute them up to arbitrary order.
Computing up to ![]()
Set the signature of spacetime such that its space part is equal to +++ and use lowercaselatin letters to represent space indices. Set also ![]() ,
, ![]() and
and ![]() to represent quantum operators
to represent quantum operators
| > |
| > |
| (199) |
To illustrate the computation up to ![]() , a convenient example, where the commutator algebra is closed, consists of taking
, a convenient example, where the commutator algebra is closed, consists of taking ![]() and
and ![]() as Pauli Matrices which, multiplied by the imaginary unit, form a basis for the
as Pauli Matrices which, multiplied by the imaginary unit, form a basis for the ![]() group, which in turn exponentiate to the relevant Special Unitary Group
group, which in turn exponentiate to the relevant Special Unitary Group ![]() . The algebra for the Pauli matrices involves a commutator and an anticommutator
. The algebra for the Pauli matrices involves a commutator and an anticommutator
| > |
| (200) |
Assign now ![]() and
and ![]() to two Pauli matrices, for instance
to two Pauli matrices, for instance
| > |
| (201) |
| > |
| (202) |
Next, to extract the coefficient of ![]() from
from
![]()
to solve it for ![]() we note that each term has a factor
we note that each term has a factor ![]() multiplying a sum, so we only need to take into account the first
multiplying a sum, so we only need to take into account the first ![]() terms (sums) and in each sum replace
terms (sums) and in each sum replace ![]() by the corresponding
by the corresponding ![]() . For example, given
. For example, given ![]() to compute
to compute ![]() we only need to compute these first three terms:
we only need to compute these first three terms:
![0 = `+`(Sum(`/`(`*`(`^`(lambda, n), `*`({B, `^`(A, n)})), `*`(factorial(n))), n = 1 .. 2), `*`(2, `*`(lambda, `*`(Sum(Sum(`/`(`*`(`^`(lambda, `+`(n, m)), `*`({C[2], `^`(A, m), `^`(B, n)})), `*`(factor...](Physics/Physics_824.gif)
then solving for ![]() one gets
one gets ![]() .
.
Also, since to compute ![]() we only need the coefficient of
we only need the coefficient of ![]() , it is not necessary to compute all the terms of each multiple-sum. One way of restricting the multiple-sums to only one power of
, it is not necessary to compute all the terms of each multiple-sum. One way of restricting the multiple-sums to only one power of ![]() consists of using multi-index summation, available in the Physics package. For that purpose, redefine sum to extend its functionality with multi-index summation
consists of using multi-index summation, available in the Physics package. For that purpose, redefine sum to extend its functionality with multi-index summation
| > |
| (203) |
Now we can represent the same computation of ![]() without multiple sums and without computing unnecessary terms as
without multiple sums and without computing unnecessary terms as
![]()
Finally, we need a computational representation for the repeated commutator bracket
![]()
One way of representing this commutator bracket operation is defining a procedure, say F, with a cache to avoid recomputing lower order nested commutators, as follows
| > |
| (204) |
For example,
| > |
| (205) |
| > |
| (206) |
| > |
| (207) |
We can set now the value of ![]()
| > |
| (208) |
and enter the formula that involves only multi-index summation
| > |
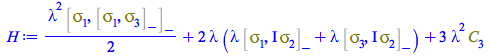 |
(209) |
from where we compute ![]() by solving for it the coefficient of
by solving for it the coefficient of ![]() , and since due to the multi-index summation this expression already contains
, and since due to the multi-index summation this expression already contains ![]() as a factor,
as a factor,
| > |
| (210) |
In order to generalize the formula for H for higher powers of ![]() , the right-hand side of the multi-index summation limit can be expressed in terms of an abstract N, and H transformed into a mapping:
, the right-hand side of the multi-index summation limit can be expressed in terms of an abstract N, and H transformed into a mapping:
| > |
| (211) |
Now we have
| > |
| (212) |
| > |
| (213) |
The following is already equal to ![]()
| > |
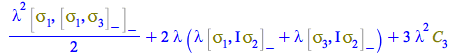 |
(214) |
In this way, we can reproduce the results published in the literature for the coefficients of Zassenhaus formula up to ![]() by adding two more multi-index sums to
by adding two more multi-index sums to ![]()
![]() . Unassign
. Unassign ![]() first
first
| > |
| > |
We compute now up to ![]() in one go
in one go
| > |
| (215) |
The nested-commutator expression solved in the last step for ![]() is
is
| > |
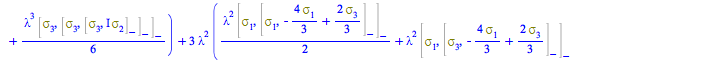 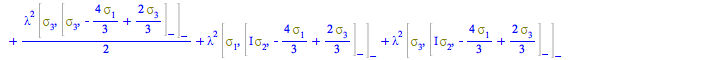 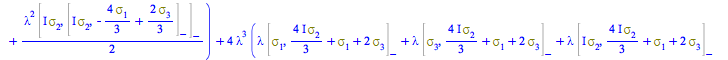 |
(216) |
With everything understood, we want now to extend these results generalizing them into an approach to compute an arbitrarily large coefficient ![]() , then use that generalization to compute all the Zassenhaus coefficients up to
, then use that generalization to compute all the Zassenhaus coefficients up to ![]() . To type the formula for H for higher powers of
. To type the formula for H for higher powers of ![]() is however prone to typographical mistakes. The following is a program, using the Maple programming language, that produces these formulas for an arbitrary integer power of
is however prone to typographical mistakes. The following is a program, using the Maple programming language, that produces these formulas for an arbitrary integer power of ![]() :
:
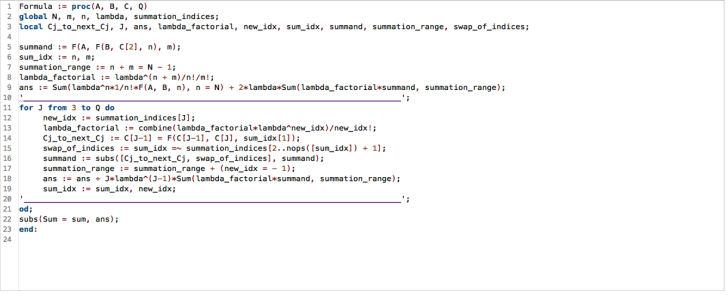
This Formula program uses a sequence of summation indices with as much indices as the order of the coefficient ![]() we want to compute, in this case we need 10 of them
we want to compute, in this case we need 10 of them
| > |
| (217) |
To avoid interference of the results computed in the loop ![]() , unassign
, unassign ![]() again
again
| > |
Now the formulas typed by hand, used lines above to compute each of ![]() ,
, ![]() and
and ![]() , are respectively constructed by the computer
, are respectively constructed by the computer
| > |
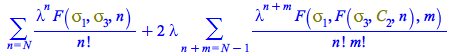 |
(218) |
| > |
| (219) |
| > |
| (220) |
Construct then the formula for ![]() and make it be a mapping with respect to N, as done for
and make it be a mapping with respect to N, as done for ![]() after
after ![]()
| > |
| (221) |
Compute now the coefficients of the Zassenhaus formula up to ![]() all in one go
all in one go
| > |
| (222) |
Notes: with the material above you can compute higher order values of ![]() . For that you need:
. For that you need:
Multivariable Taylor series of expressions involving anticommutative (Grassmannian) variables
The Physics:-Gtaylor command, for computing Taylor series of expressions involving anticommutative variables, got rewritten, now as a multivariable Taylor series command (same difference as in between the taylor and mtaylor commands) and combining two different approaches to handle, when possible, the presence of noncommutative and anticommutative variables. One is the standard approach for multi-variable expansions, it requires that the derivative of each function entering the expression being expanded commutes with the function itself. The second approach, for expansions with respect to anticommutative variables, separates the function into a "Body" and a "Soul", as is standard in supermathematics.
Consider a set of anticommutative Grassmann variables ![]() with
with ![]() , forming a basis enlarged by their products, that satisfies
, forming a basis enlarged by their products, that satisfies ![]() , so that
, so that ![]() The elements of the algebra involving these variables are linear combinations of the form
The elements of the algebra involving these variables are linear combinations of the form
![]()
where the coefficients ![]() are complex numbers,
are complex numbers, ![]() is called the body and everything else,
is called the body and everything else, ![]() , is called the soul (nilpotent part).
, is called the soul (nilpotent part).
Consider now a mapping (function) ![]() which is assumed to be differentiable. Then
which is assumed to be differentiable. Then ![]() can be defined by its Taylor expansion,
can be defined by its Taylor expansion,
![]()
That is the expansion computed by Gtaylor in Maple 2019.
Examples
| > |
| (223) |
Consider
| > |
| (224) |
Step by step, ![]() is the application of the mapping
is the application of the mapping
| > |
| (225) |
to the element of the algebra
| > |
| (226) |
The body of ![]() is
is
| > |
| (227) |
The soul of ![]() is
is
| > |
| (228) |
and in view of
| > |
| (229) |
for the expression ![]() , the Taylor expansion, mentioned in the introductory paragraph is
, the Taylor expansion, mentioned in the introductory paragraph is
| > |
| (230) |
The same computation, all in one go:
| > |
| (231) |
Problem. Taking into account that, with regards to Grassmann variables, differentiation and integration are the same operation, recover the determinant of the coefficient matrix with dimension ![]()
Define the coefficient matrix and construct the exponential
| > |
| > |
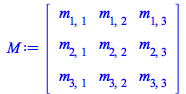 |
(232) |
| > |
| (233) |
| > |
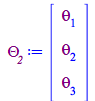 |
(234) |
| > |
| (235) |
The integral of this exponential can thus be obtained performing a multivariable Taylor series expansion, then differentiating (equivalent to integrating) with respect to the six ![]() variables.
variables.
| > |
To avoid the default behavior of discarding terms of order 6 or higher in ![]() , as in the other
series
commands of the Maple system, indicate the order term to be
, as in the other
series
commands of the Maple system, indicate the order term to be ![]() .
.
| > |
| (236) |
Perform now the integration of the expanded exponential
| > |
| (237) |
Compare with the determinant of the coefficient matrix M
| > |
| (238) |
| > |
| (239) |
| > |
| (240) |
Define corresponding annihilation and creation operators
| > |
| (241) |
| > |
| (242) |
Note that the anticommutator of these two operators is equal to 1 (so they don't anticommute)
| > |
| (243) |
while they do anticommute with all Grassmann variables
| > |
| (244) |
| > |
| (245) |
and, because of Pauli's exclusion principle for fermions, the square of ![]() and
and ![]() are equal to 0.
are equal to 0.
Consider now the product of exponentials
| > |
| (246) |
Because the corresponding exponents ![]() and
and ![]() commute with their commutator, this product of exponentials can be combined using Hausdorff's formula
commute with their commutator, this product of exponentials can be combined using Hausdorff's formula
| > |
| (247) |
Both sides can be expanded in multivariable Taylor series, this time including the annihilation and creation operators as series variables since their commutation rules are all known (![]() ,
, ![]() ,
, ![]() ) and their square is equal to 0:
) and their square is equal to 0:
| > |
| (248) |
On the left-hand side is the product of the expansion of each exponential while on the right-hand side it is the expansion of the single exponential (no-trivially) combined taking into account the commutator of the exponents on the left-hand side. Verify that both expansions are one and the same:
| > |
| (249) |
| > |
| (250) |
| > |
| (251) |
| > |
| (252) |
| > |
| (253) |
| > |
| (254) |
| > |
| (255) |
| > |
New SortProducts command
A new command, SortProducts, receives an expression involving products and sorts the operands of these products according to the ordering indicated as the second argument, a list containing some or all of the operands of the product(s) found in the expression. The sorting of operands performed automatically takes into account any algebra rules set using Setup.
Examples
| > |
| > |
Consider the product of the commutative ![]()
| > |
| (256) |
Reorder the operands ![]() and
and ![]() "in place".
"in place".
| > |
| (257) |
Sort the operands ![]() and
and ![]() and put them to the left, then to the right
and put them to the left, then to the right
| > |
| (258) |
| > |
| (259) |
Set a prefix identifying noncommutative variables and related algebra rules for some of them, such that ![]() and
and ![]() commute between themselves, but none of them commute with
commute between themselves, but none of them commute with ![]() .
.
| > |
| (260) |
| > |
| (261) |
Sort Z2 and Z3 "in place".
| > |
| (262) |
| > |
| (263) |
The value of the commutator between Z1 and Z5 is not known to the system, so by default they are not sorted:
| > |
| (264) |
Force their sorting using their commutator or anticommutator
| > |
| (265) |
| > |
| (266) |
| > |
| (267) |
| > |
| (268) |
Enter the product of ![]() with
with ![]() at the end (so, to the right of P) and sort it with
at the end (so, to the right of P) and sort it with ![]() to the left. This is a case where
to the left. This is a case where ![]() does not commute with any of the other operands. Compare the results with and without the option usecommutator,
does not commute with any of the other operands. Compare the results with and without the option usecommutator,
| > |
| (269) |
| > |
| (270) |
| > |
| (271) |
| > |
| (272) |
Documentation: "Physics updates", "A complete guide for performing tensor computations" and the "Mini-Course: Computer Algebra for Physicists"
Simplification of tensors, Pauli and Dirac matrices and KroneckerDelta
A new algorithm for normalizing tensorial expressions got implemented, following the ideas presented in the paper by L. R. U. Manssur, R. Portugal, and B. F. Svaiter,
Group-Theoretic Approach for Symbolic Tensor Manipulation, International Journal of Modern Physics C, Vol. 13, No. 07, pp. 859-879 (2002).
Examples
| > |
| (273) |
Define the following tensors, with no particular symmetry
| > |
| (274) |
These tensors, A, B, F, H, and J respectively depend on 1 to 5 indices in the following tensorial expressions, all of which are actually equal to 0. The simplifier in Maple 2019 detects that fact by rewriting these expressions in the canonical / normal form explained in the reference mentioned above. To input the expressions with the contravariant indices as superscripts, type them preceded by ~, then right-click the input expression and select 2-D Math → Convert To → 2-D Math Input.
| > |
| > |
| (275) |
| > |
| > |
| (276) |
| > |
| > |
| (277) |
| > |
| > |
| (278) |
The following example is less simple, define a tensor with three indices, that is symmetric with respect to the last two of them
| > |
| (279) |
So
| > |
| (280) |
| > |
| (281) |
If we now swap ![]() with
with ![]() and take the difference we get an antisymmetric tensorial expression
and take the difference we get an antisymmetric tensorial expression
| > |
| (282) |
So, by construction, the following is equal to 0 even when none of the terms is; detecting situations like this one is part of the intrinsic efficiency of the group theoretic approach
| > |
| (283) |
| > |
| (284) |
In Maple 2019, to compute the matrix components use Library:-RewriteInMatrixForm and Library:-PerformMatrixOperations
| > |
| (285) |
Since Pauli matrices are now defined as a 4-vector, all the keywords for tensors automatically work
| > |
| (286) |
Likewise, you can visualize tensor components the usual way using TensorArray
| > |
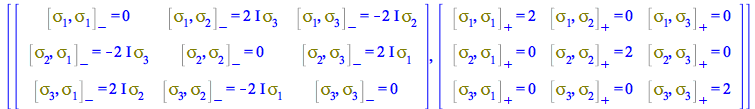 |
(287) |
To see the matrix expression of these commutators and anticommutators of Pauli matrices use the option performmatrixoperations. For example, for the first block of identities involving commutators,
| > |
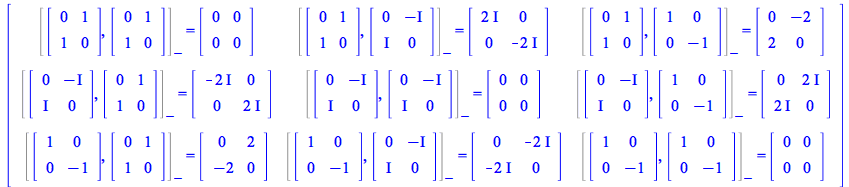 |
(288) |
The simplifier now knows more about Pauli matrices
| > |
| (289) |
| > |
| (290) |
| > |
| (291) |
| > |
| (292) |
| > |
| (293) |
| > |
| (294) |
These two library routines are the ones used to rewrite tensorial expressions in matrix form or to perform the corresponding matrix operations
| > |
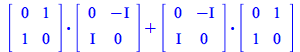 |
(295) |
| > |
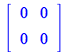 |
(296) |
The same works for the Dirac matrices
| > |
| (297) |
| > |
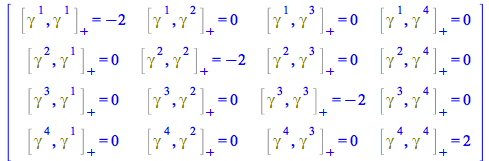 |
(298) |
New in Maple 2019, when Physics is loaded the standard representation of Dirac matrices is automatically loaded too, corresponding to the contravariant components of ![]()
| > |
| (299) |
| > |
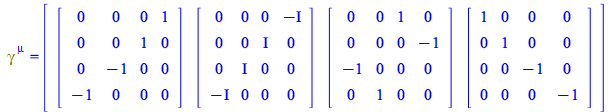 |
(300) |
The definition of ![]() is also visible using the keyword definition
is also visible using the keyword definition
| > |
| (301) |
Verify the first three of these identities
| > |
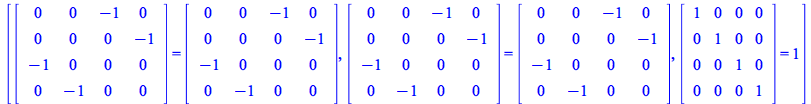 |
(302) |
For the fourth identity
| > |
| (303) |
| > |
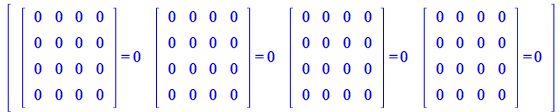 |
(304) |
You can compute with the tensor components and later represent them in matrix form, or perform the corresponding matrix operations
| > |
| (305) |
| > |
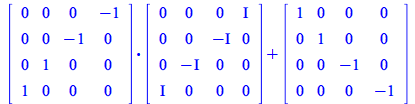 |
(306) |
| > |
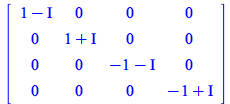 |
(307) |
| > |
| (308) |
| > |
| (309) |
| > |
 |
(310) |
| > |
 |
(311) |
Although in an Euclidean space the Kronecker ![]() symbol is a tensor, its components do not change under a transformation of coordinates, that is not the case in a Minkowski or curved spacetime. Also, KroneckerDelta is more often than otherwise used taking
symbol is a tensor, its components do not change under a transformation of coordinates, that is not the case in a Minkowski or curved spacetime. Also, KroneckerDelta is more often than otherwise used taking ![]() when
when ![]() , while due to Einstein's sum rule for repeated indices, if KroneckerDelta were a tensor and
, while due to Einstein's sum rule for repeated indices, if KroneckerDelta were a tensor and ![]() is a tensor index, then
is a tensor index, then ![]() . To avoid this ambiguity of notation, in Maple 2019 KroneckerDelta is not implemented as a tensor, but as the standard non-tensorial Kronecker
. To avoid this ambiguity of notation, in Maple 2019 KroneckerDelta is not implemented as a tensor, but as the standard non-tensorial Kronecker ![]() symbol.
symbol.
For the cases where you need to use it as a tensor, for example when entering commutation relations in quantum mechanics using tensorial notation, you can either use the metric itself ![]() , or define a Kronecker
, or define a Kronecker ![]() tensor for that purpose. For example
tensor for that purpose. For example
| > |
| (312) |
This does not return the dimension of space
| > |
| (313) |
This returns the dimension of space:
| > |
| (314) |
You can define a Kronecker delta; tensor using Define with ease, for example defining the covariant components of the tensor as follows
| > |
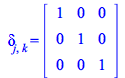 |
(315) |
| > |
| (316) |
Now you have
| > |
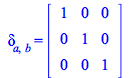 |
(317) |
| > |
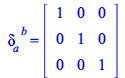 |
(318) |
| > |
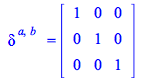 |
(319) |
And the trace:
| > |
| (320) |
So this is not equal to 1
| > |
| (321) |
| > |
| (322) |
This ![]() tensor, well defined in an Euclidean space, however changes when the space is not Euclidean. For example:
tensor, well defined in an Euclidean space, however changes when the space is not Euclidean. For example:
| > |
| (323) |
| > |
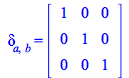 |
(324) |
| > |
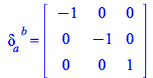 |
(325) |
| > |
| (326) |