
Maple 2020 includes many new additions designed to support learning and teaching Linear Algebra.
![]()
Step-by-Step Solutions for Tutors
A much-requested feature, the Gaussian Elimination, Gauss-Jordan Elimination, and Matrix Inverse tutors all now return the step-by-step solutions from the tutor to the Maple worksheet.
![GaussJordanEliminationTutor(rtable(1 .. 3, 1 .. 4, [[1, 0, 0, 3], [2, 1, 2, 5], [0, 2, 1, 5]], subtype = Matrix));](learningtools-linearalgebra/LearningToolsForLinearAlgebra_2.gif)
![rtable(1 .. 3, 1 .. 4, [[1, 0, 0, 3], [2, 1, 2, 5], [0, 2, 1, 5]], subtype = Matrix);](learningtools-linearalgebra/LearningToolsForLinearAlgebra_3.gif) |
| Add -2 times row 1 to row 2: |
![rtable(1 .. 3, 1 .. 4, [[1, 0, 0, 3], [0, 1, 2, -1], [0, 2, 1, 5]], subtype = Matrix);](learningtools-linearalgebra/LearningToolsForLinearAlgebra_4.gif) |
| Add -2 times row 2 to row 3: |
![rtable(1 .. 3, 1 .. 4, [[1, 0, 0, 3], [0, 1, 2, -1], [0, 0, -3, 7]], subtype = Matrix);](learningtools-linearalgebra/LearningToolsForLinearAlgebra_5.gif) |
| Multiply row 3 by -1/3: |
![rtable(1 .. 3, 1 .. 4, [[1, 0, 0, 3], [0, 1, 2, -1], [0, 0, 1, -`/`(7, 3)]], subtype = Matrix);](learningtools-linearalgebra/LearningToolsForLinearAlgebra_6.gif) |
| Add -2 times row 3 to row 2: |
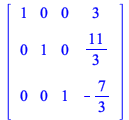 |
Context Panel Options
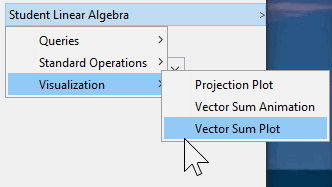
Many visualizations have been added to the Student:-LinearAlgebra context panel, including CrossProductPlot, EigenPlot, LeastSquaresPlot, LinearSystemPlot, LinearTransformPlot, PlanePlot, ProjectionPlot, and VectorSumPlot (plot or animation).
For example, clicking on each output below and selecting from the options in the context panel, you can quickly generate the following plots:
|
|
||||
|
|
The context panel options have also been simplified to show fewer items than before when the Student:-LinearAlgebra package is loaded.
New Commands
Several of these new commands call commands from the LinearAlgebra package, however they have been slightly modified to suit the Student:-LinearAlgebra package.
For example, the LinearAlgebra:-MatrixInverse command returns results for square and non-square matrices. In Student:-LinearAlgebra, this command has been split into two commands: MatrixInverse, which only works for square matrices, and Pseudoinverse, which works for non-square matrices.
![MatrixInverse(rtable(1 .. 2, 1 .. 2, [[1, 2], [3, 1]], subtype = Matrix));](learningtools-linearalgebra/LearningToolsForLinearAlgebra_29.gif)
 |
![Pseudoinverse(rtable(1 .. 2, 1 .. 3, [[3, -2, -3], [1, 2, -1]], subtype = Matrix));](learningtools-linearalgebra/LearningToolsForLinearAlgebra_31.gif)
 |