Maple
Powerful math software that is easy to use
• Maple for Academic • Maple for Students • Maple Learn • Maple Calculator App • Maple for Industry and Government • Maple Flow • Maple for Individuals
Maple 2020 improves the performance of several key functions.
In Maple 2020, the natural logarithm of large integers computes much faster and with less memory.
On an i7-8650U processor, Maple 2020 computes the following in about 14 seconds. Maple 2019, however, takes 17 minutes
 |
| memory used=3.99GiB, alloc change=244.86MiB, cpu time=15.14s, real time=15.21s, gc time=15.62ms
|
 |
This directly translates to performance gains in computing logarithms in all integer bases, as they work by computing natural logarithms.
The factorial function is faster for large arguments. This case is about three times faster than in Maple 2019.
| memory used=230.57MiB, alloc change=26.75MiB, cpu time=765.00ms, real time=759.00ms, gc time=0ns
|
 |
Integer Least Common Multiple
The integer least common multiple function (ilcm) has become much faster when called many times on smaller arguments. The following case is about ten times faster than in Maple 2019.
| memory used=62.21MiB, alloc change=-110.98MiB, cpu time=562.00ms, real time=538.00ms, gc time=62.50ms
|
Integration in the VectorCalculus and MultivariateCalculus Packages
The integration commands from the VectorCalculus and MultivariateCalculus packages (and the corresponding Student subpackages) now use the collapsed rather than the nested form for multiple integration. This allows the outer integration steps to use and benefit directly from the knowledge of the ranges of the inner integration steps.This allows computation to complete more quickly for some examples, and to succeed in some examples which previously did not succeed or which required special assumptions to be made. The following example now computes in under one second, on a machine where previously it took 100 seconds unless executed under the assumption that abs(y)<z .
The following example now computes in approximately one second, whereas previously it used a prohibitively large amount of time and memory resources.
![MultiInt(sqrt(`*`(x, `*`(y))), [x, y, z] = Tetrahedron(`<,>`(0, 0, 0), `<,>`(1, 0, 0), `<,>`(0, 1, 0), `<,>`(0, 0, 1)));](performance/Performance_13.gif){kind=small}
The following examples erroneously returned 0 in Maple2019.
![int(`/`(`*`(exp(`+`(x, `*`(I, `*`(y))))), `*`(`+`(1, `-`(x), `*`(I, `*`(y))))), [x, y] = Circle(`<,>`(0, 0), 1));](performance/Performance_16.gif){kind=small}
 |
![int(`*`(exp(x), `*`(cos(y))), [x, y] = Circle(`<,>`(0, 0), 1));](performance/Performance_18.gif){kind=small}
 |
The following example now computes in a few seconds, but did not complete in Maple 2019.
![int(`/`(1, `*`(`+`(`*`(`^`(x, 2)), `*`(`^`(y, 2)), `*`(`^`(z, 2))))), [x, y, z] = Sphere(`<,>`(2, 0, 0), 1));](performance/Performance_20.gif){kind=small}
 |
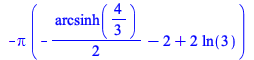The underlying structure of the returned inert form illustrates the change in behavior.
![Ex := int(`/`(1, `*`(`+`(`*`(`^`(x, 2)), `*`(`^`(y, 2)), `*`(`^`(z, 2))))), [x, y, z] = Sphere(`<,>`(2, 0, 0), 1), inert);](performance/Performance_22.gif){kind=small}
 |
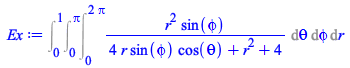| Int(r^2*sin(phi)/(4*r*sin(phi)*cos(theta)+r^2+4),[theta = 0 .. 2*Pi, phi = 0 ..
Pi, r = 0 .. 1]) |
Previously the inert form would consist of multiple, nested calls to Int.
| Int(Int(Int(r^2*sin(phi)/(4*r*sin(phi)*cos(theta)+r^2+4),theta = 0 .. 2*Pi),phi= 0 .. Pi),r = 0 .. 1) |
