
Maple 2020 includes the following visualization updates.
Plot size
The default plot size for 2-D and 3-D plots is bigger, for better visibility on high resolution monitors.
![]()
![]()
![]()
 |
In addition, the size option is now supported for 3-D plotting commands. This allows for specifying precise and consistent dimensions for the plotting window that encapsulates inline 3-D plots. This geometry is respected upon export of the plot to an image file.
The size option is also supported by the plots:-display command for combining multiple 3-D plots.
![]()
 |
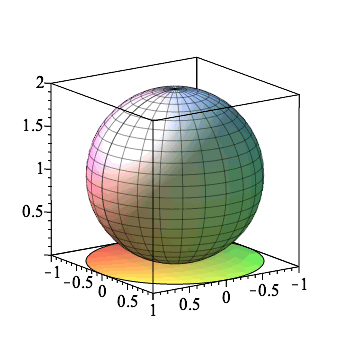
The following plot has also been manually zoomed and panned.
![]()
 |
![]()
 |
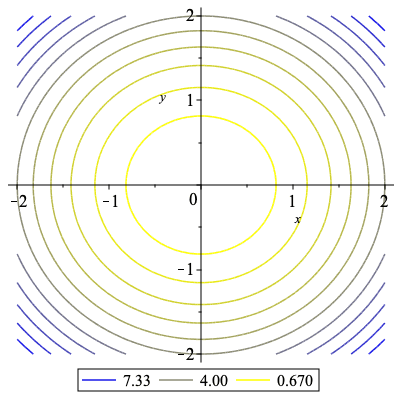
Legends for 2-D contour plots
The plots:-contourplot command's support for the legend option now allows for both automatic generated and customized legend entries to display the values of the contour lines.
![]()
![]()
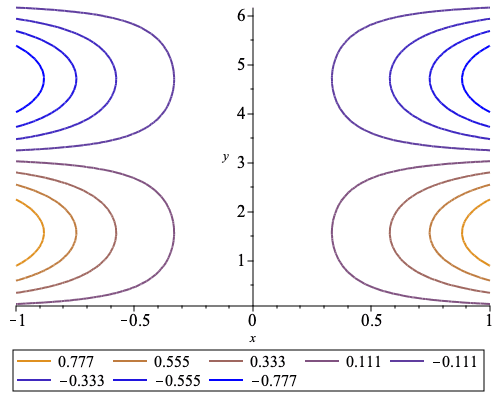 |
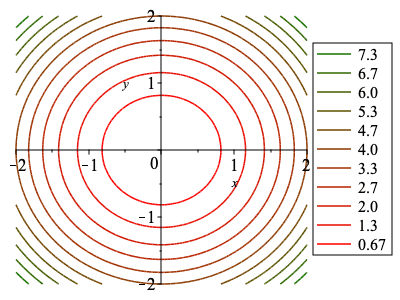
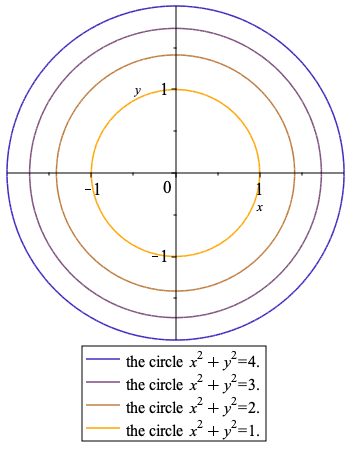
When supplied as a list the number of legend entries must match the requested number of contour lines. The contour values can be numerically formatted.
![]()
![]()
![]()
![]()
 |
The special name contourvalue can be used within a typeset formula.
![]()
![]()
![]()
 |
The special value "null" can be used to suppress the legend entry for particular contours.
![]()
![]()
![]()
![]()
![]()
![]()
 |
Adaptive edge computation for plot3d
The new adaptmesh option of the plot3d command provides for automatic adjustment of the independent values of the data points in order to display smoother edges for surfaces which are non-numeric in some part of the specified rectangular domain.
In previous releases, the surface appeared as it now does with the option given as adaptmesh=false. The new default behavior is adaptmesh=true. In the following two graphs, the default behavior in Maple 2020 is shown on the right.
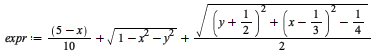
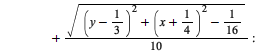
![]()
![]()
![]()
![]()
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
With the option set to true the result contains a MESH structure, while with the option set to false the result contains a GRID structure.
The data values can still be extracted using the plottools:-getdata command.
![]()
![]()
![]()
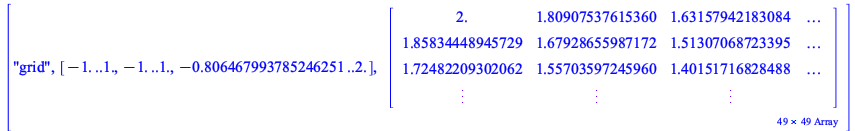 |
![]()
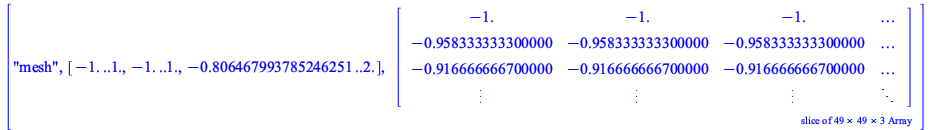 |
![]()
plottools[triangulate]
The triangulate command takes a POLYGONS or POINTS structure and return a POLYGONS structure containing a set of triangles which cover the region defined by its input.
![]()
![]()
![]()
![]()
  |
![]()
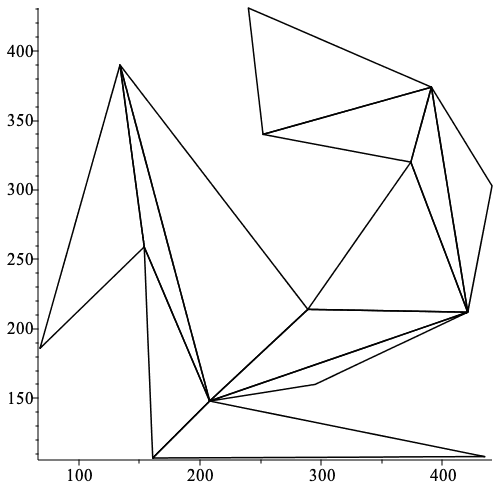 |
ColorTools:-CVDSimulation
CVDSimulation in the ColorTools package is a new command that returns how a color could be perceived by a viewer with a specific color vision deficiency.
| > |
| > |
| > |
| > |
| > |