The second illustration of the new functionality in the DifferentialGeometry package for Maple 17 also involves the exceptional Lie algebra ![g[2]](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_57.gif) , but now in the context of infinitesimal holonomy. , but now in the context of infinitesimal holonomy.
Let 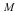 be an be an 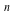 -dimensional Riemannian manifold with metric -dimensional Riemannian manifold with metric 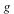 . .
Let 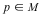 be a fixed point. be a fixed point.
Then the holonomy group Hol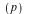 of the Riemannian manifold of the Riemannian manifold 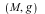 is the group of linear transformations is the group of linear transformations 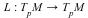 defined by the parallel transport of vectors around closed loops starting at defined by the parallel transport of vectors around closed loops starting at 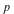 . The Lie algebra of the holonomy group is called the infinitesimal holonomy . According to the Ambrose-Singer Theorem, the infinitesimal holonomy can be computed in terms of the curvature tensor of the metric . The Lie algebra of the holonomy group is called the infinitesimal holonomy . According to the Ambrose-Singer Theorem, the infinitesimal holonomy can be computed in terms of the curvature tensor of the metric 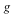 and the covariant derivatives of the curvature tensor. For many years it was an open problem in differential geometry as to whether or not there was a metric whose infinitesimal holonomy was the exceptional Lie algebra and the covariant derivatives of the curvature tensor. For many years it was an open problem in differential geometry as to whether or not there was a metric whose infinitesimal holonomy was the exceptional Lie algebra 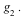 This question was answered in the affirmative by R. Bryant in 1987. This question was answered in the affirmative by R. Bryant in 1987.
In this example, use the new command InfinitesimalHolonomy to verify an example of a metric with infinitesimal holonomy g[2]; (due to S. Salamon).
First, define coordinates for a 7-dimensional manifold 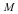 : :
| > |
![DGsetup([x1, x2, x3, x4, x5, x6, u], M)](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_69.gif) |
The computations for this example are much more easily performed in an anholonomic frame. Set:
Calculate the structure equations for this co-frame and initialize:
| > |
![FD := FrameData([o1, o2, o3, o4, o5, o6, o7], P)](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_85.gif) |
| > |
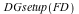 |
The metric you will study is:
| > |
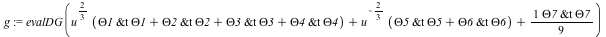 |
This metric is Ricci flat.
| > |
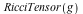 |
The infinitesimal holonomy is 14-dimensional.
| > |
![Hol := InfinitesimalHolonomy(g, [u = 1, x1 = 0, x2 = 0, x3 = 0, x4 = 0, x5 = 0, x6 = 0]); -1](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_93.gif) |
| > |
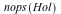 |
The holonomy algebra is easier to display if you first use the command CanonicalBasis to transform the output to standard form and then make the change of variables u = t^3.
| > |
![Hol1 := `assuming`([simplify(subs(u = `*`(`^`(t, 3)), Tools:-CanonicalBasis(Hol)))], [`<`(0, t)])](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_96.gif) |
| > |
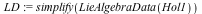 |
You can now proceed as in Example 1 to show that this Lie algebra is also the exceptional Lie algebra ![g[2]](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_114.gif) . .
Finally, you can use CovariantlyConstantTensors and the new command InvariantTensorsAtAPoint to show that the metric above admits a covariantly constant (parallel) 3-form. Any covariantly constant 3-form must be pointwise invariant with respect to the infinitesimal holonomy algebra. First find these invariant 3-forms.
| > |
![Omega := Tools:-GenerateForms([Theta1, Theta2, Theta3, Theta4, Theta5, Theta6, Theta7], 3)](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_115.gif) |
| P > |
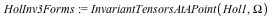 |
In terms of the original coordinate 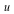 this becomes: this becomes:
| > |
![alpha0 := subs(t = `*`(`^`(u, `/`(1, 3))), HolInv3Forms[1])](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_125.gif) |
Every covariantly constant 3-form must be a multiply of this form so use this as the ansatz which you pass to the command CovariantlyConstantTensors.
| > |
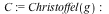 |
| > |
![alpha := CovariantlyConstantTensors(g, ansatz = evalDG(`*`(f(u), `*`(alpha0))), unknowns = [f(u)])](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_129.gif) |
| > |
![CovariantDerivative(alpha[1], C)](/products/maple/new_features/images17/DifferentialGeometry/DifferentialGeometry_132.gif) |
|
