Maple 16 provides improved linearization routines which greatly facilitate the process of integrating a linearized system into your original model. In previous releases, users had to include the derivative of the input when linearizing their system. This resulted in the addition of an extra input which required users to manipulate the structure of their model in order to accommodate their newly linearized system. In Maple 16, users can apply the linearization routines without any post-processing. A non-linear model with one input and one output will continue to have the the same I/O configuration.
In addition to improvements to linearization, Maple 16 offers built-in support for Nichols plots, further extending the analysis and computation capabilities for control design. |
|
Nichols Plots
Maple 16 offers built-in support for Nichols plots. Below is a Nichols plot of a closed-loop system with unity feedback. Select frequencies are labeled.

Linearization in Maple 16
The example below uses the model of a controlled electrical power source driving a capacitor with a series resistor and a parallel resistance load to illustrate the improvements to the linearization command in Maple 16.
The equations of this system can be defined as:
| > |
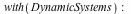 |
| > |
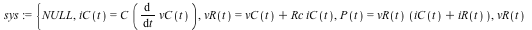
 |
The linearization points for the system are:
| > |
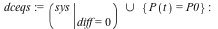 |
| > |
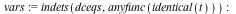 |
| > |
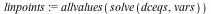 |
| > |
![linpoint1 := linpoints[1]](/products/maple/new_features/images16/ControlDesign_12.gif) |
In Maple 15, if we attempted to linearize this system would obtain the following error message:
| > |
![lin, smap, imap, omap := Linearize(sys, [P(t)], [vR(t)], linpoint1)](/products/maple/new_features/images16/ControlDesign_14.gif) |
The reason for this message was that the derivative of input function,  , needed to be included in the linearization point. This resulted in a linearized system with one extra input as compared to the original non-linear system. , needed to be included in the linearization point. This resulted in a linearized system with one extra input as compared to the original non-linear system.
| > |
![lin, smap, imap, omap := Linearize(sys, [P(t)], [vR(t)], `union`(linpoint1, {(D(P))(t) = 0}))](/products/maple/new_features/images16/ControlDesign_16.gif) |
In Maple 16, we are able to linearize the system without specifying the derivate of the input function. As a result, the linearized system has the same number of inputs and outputs as the non-linear model, enabling the user to incorporate the linearized system into the original model with modification.
| > |
![lin, smap, imap, omap := Linearize(sys, [P(t)], [vR(t)], linpoint1)](/products/maple/new_features/images16/ControlDesign_19.gif) |
|
