New Features in Maple 17: Signal Processing
 

 Next Feature

Introduction 

Maple 17 offers new signal processing tools for analyzing and manipulating data in the frequency and time domains. It can be used for diverse applications such as creating a speech spectrogram, removing noise from polluted signals, and identifying the periodicity of data.  

This package includes tools for: 

  • Cosine, fast Fourier and wavelet transforms 
  • Bartlett, Blackman, Kaiser, Hann, and Hanning windows 
  • Signal generation  
  • Cross-correlation, autocorrelation, data statistics, and upsampling/downsampling 
  • FIR, IIR, and Butterworth filters 
> with(SignalProcessing[Engine])
 







 
 

Application: Imaging a Speech Spectrogram

Import Wave File and Manipulate Data into Overlapping Slices

>

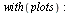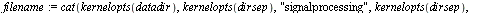
> filename := cat(kernelopts(datadir), kernelopts(dirsep),
filename := cat(kernelopts(datadir), kernelopts(dirsep),

C:\Program Files\Maple 17\data\signalprocessing\maplesim.wav  

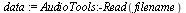> data := AudioTools:-Read(filename)

data := Vector[column](%id = 4361768386)  

>

11025  

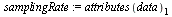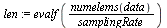> len := evalf(`/`(`*`(numelems(data)), `*`(samplingRate)))

.7462131519  


Slice the data into segments with 256 samples. Each slice has a 50% overlap with the previous slice (that is, each slice starts at the half-way point of the previous slice). 

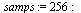> samps := 256; -1
 
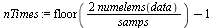> nTimes := `+`(floor(`+`(`/`(`*`(2, `*`(numelems(data))), `*`(samps)))), `-`(1))
 
63  
 
> sample := Matrix(samps, nTimes, proc (i, j) options operator, arrow; data[`+`(i, `*`(`/`(1, 2), `*`(`+`(j, `-`(1)), `*`(samps))))] end proc, datatype = float[8]); 1
 
sample := Vector[column](%id = 4524928962)  
 

Calculate the Spectrogram Data 

Filter the data, slice by slice. 

> a := `<|>`(`<,>`(seq(HannWindow(sample[() .. (), i]), i = 1 .. nTimes))); -1
 

Calculate FFT of time segment consecutively. 

> FFTa := `<|>`(`<,>`(seq(FFT(a[i, () .. ()]), i = 1 .. nTimes))); -1
 

Calculate Power Spectrum of each slice consecutively. 

> spectra := `<|>`(`<,>`(seq(`~`[sqrt](PowerSpectrum(FFTa[i, () .. ()])), i = 1 .. nTimes))); -1
 

Convert spectrum into decibels. 

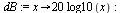> dB := proc (x) options operator, arrow; `+`(`*`(20, `*`(log10(x)))) end proc; -1
 
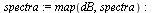> spectra := map(dB, spectra); -1
 

Strip out the repeated data. 

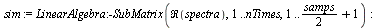> sim := LinearAlgebra:-SubMatrix(Re(spectra), 1 .. nTimes, 1 .. `+`(`*`(`/`(1, 2), `*`(samps)), 1)); -1
 
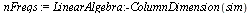> nFreqs := LinearAlgebra:-ColumnDimension(sim)
 
129  
 

The frequencies go from 0 to half the sampling rate. Hence the frequencies are in steps of (in Hz): 

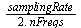> `*`(samplingRate, `*`(`/`(`+`(`*`(2., `*`(nFreqs))))))
 
42.73255814  
 

Scale the spectra so that the values are between 0 and 255. 

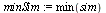> minSim := min(sim)
 
HFloat(-111.18888523873858)  
 
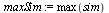> maxSim := max(sim)
 
HFloat(4.43801796851939)  
 
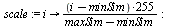> scale := proc (i) options operator, arrow; `/`(`*`(`+`(`*`(255, `*`(i)), `-`(`*`(255, `*`(minSim))))), `*`(`+`(maxSim, `-`(minSim)))) end proc; -1
 

Consecutive rows represent slices in time, while columns contain the spectra at each time. 

> simScaled := `~`[scale](sim); 1
 
simScaled := Vector[column](%id = 4524921090)  
 

Plot the Spectrogram and Waveform 

> commonPlotOpts1 := labelfont = [Helvetica], labeldirections = [horizontal, vertical]; -1
 
> p1 := listdensityplot(`+`(`-`(simScaled)), style = patchnogrid, smooth = true, tickmarks = [[], [seq(i = `*`(round(`+`(`*`(10, `*`(samplingRate, `*`(i, `*`(`/`(`+`(`*`(2000., `*`(nFreqs)))))))))), `*`...
p1 := listdensityplot(`+`(`-`(simScaled)), style = patchnogrid, smooth = true, tickmarks = [[], [seq(i = `*`(round(`+`(`*`(10, `*`(samplingRate, `*`(i, `*`(`/`(`+`(`*`(2000., `*`(nFreqs)))))))))), `*`...
p1 := listdensityplot(`+`(`-`(simScaled)), style = patchnogrid, smooth = true, tickmarks = [[], [seq(i = `*`(round(`+`(`*`(10, `*`(samplingRate, `*`(i, `*`(`/`(`+`(`*`(2000., `*`(nFreqs)))))))))), `*`...
 
> p2 := listplot([seq([`/`(`*`(i), `*`(samplingRate)), data[i]], i = 1 .. numelems(data))], thickness = 0, gridlines, axes = boxed, labels = [
p2 := listplot([seq([`/`(`*`(i), `*`(samplingRate)), data[i]], i = 1 .. numelems(data))], thickness = 0, gridlines, axes = boxed, labels = [
 
> display(Array(`<|>`(`<,>`(p1, p2))), aligncolumns = [1])
 

Plot_2d
Plot_2d

Application: Filtering Audio 

Import Speech Sample 

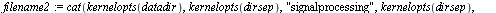
> filename2 := cat(kernelopts(datadir), kernelopts(dirsep),
filename2 := cat(kernelopts(datadir), kernelopts(dirsep),
 
C:\Program Files\Maple 17\data\signalprocessing\MapleSimMono11025.wav  
 
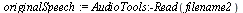> originalSpeech := AudioTools:-Read(filename2)
 
originalSpeech := Vector[column](%id = 4524921794)  
 

Plot Waveform and Power Spectrum 

> commonPlotOpts2 := titlefont = [Helvetica, 12], labelfont = [Helvetica], labeldirections = [horizontal, vertical], axis = [gridlines = [color =
commonPlotOpts2 := titlefont = [Helvetica, 12], labelfont = [Helvetica], labeldirections = [horizontal, vertical], axis = [gridlines = [color =
 
> samplingRate := attributes(originalSpeech)[1]
 
11025  

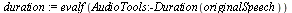> duration := evalf(AudioTools:-Duration(originalSpeech))
 
4.504671202  
 
> p1 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), originalSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, title =
p1 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), originalSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, title =
p1 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), originalSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, title =
p1 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), originalSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, title =
 
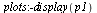> plots:-display(p1)
 
Plot_2d
 
> fq := FFT(originalSpeech[1 .. `^`(2, 15)]); -1
 
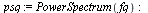> psq := PowerSpectrum(fq); -1
 
> ps1 := plots:-pointplot([seq([`/`(`*`(i, `*`(samplingRate)), `*`(`^`(2, 15))), psq[i]], i = 1 .. `+`(`*`(`/`(1, 2), `*`(`^`(2, 15)))))], thickness = 0, color = black, gridlines, connect = true, title ...
ps1 := plots:-pointplot([seq([`/`(`*`(i, `*`(samplingRate)), `*`(`^`(2, 15))), psq[i]], i = 1 .. `+`(`*`(`/`(1, 2), `*`(`^`(2, 15)))))], thickness = 0, color = black, gridlines, connect = true, title ...
ps1 := plots:-pointplot([seq([`/`(`*`(i, `*`(samplingRate)), `*`(`^`(2, 15))), psq[i]], i = 1 .. `+`(`*`(`/`(1, 2), `*`(`^`(2, 15)))))], thickness = 0, color = black, gridlines, connect = true, title ...
ps1 := plots:-pointplot([seq([`/`(`*`(i, `*`(samplingRate)), `*`(`^`(2, 15))), psq[i]], i = 1 .. `+`(`*`(`/`(1, 2), `*`(`^`(2, 15)))))], thickness = 0, color = black, gridlines, connect = true, title ...
 
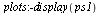> plots:-display(ps1)
 
Plot_2d
 

 

Apply IIR Butterworth or Chebyshev Filter 

Apply Filter 

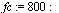> fc := 800; -1
 
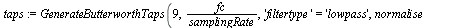
> taps := GenerateButterworthTaps(9, `/`(`*`(fc), `*`(samplingRate)), 'filtertype' = 'lowpass', normalise = true)
taps := GenerateButterworthTaps(9, `/`(`*`(fc), `*`(samplingRate)), 'filtertype' = 'lowpass', normalise = true)
 
taps := Vector[column](%id = 4524922882)  
 
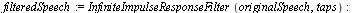> filteredSpeech := InfiniteImpulseResponseFilter(originalSpeech, taps); -1
 

View Before and After Power Spectrum and Waveform 

> FFTfilteredSpeech := FFT(filteredSpeech[1 .. `^`(2, 15)]); -1
 
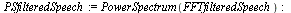> PSfilteredSpeech := PowerSpectrum(FFTfilteredSpeech); -1
 
>


 
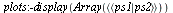> plots:-display(Array(`<,>`(`<|>`(ps1, ps2))))
 

Plot_2d Plot_2d

 
> p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
 
> plots:-display(Array(`<,>`(`<|>`(p1, p2))), view = [0 .. duration, -1 .. 1])
 

Plot_2d Plot_2d

 

Apply FIR Filter 

Apply Filter 

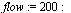> flow := 200; -1
 
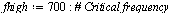> fhigh := 700; -1
 
>
 
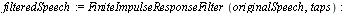> filteredSpeech := FiniteImpulseResponseFilter(originalSpeech, taps); -1
 

View Before and After Power Spectrum and Waveform 

> FFTfilteredSpeech := FFT(filteredSpeech[1 .. `^`(2, 15)]); -1
 
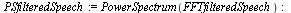> PSfilteredSpeech := PowerSpectrum(FFTfilteredSpeech); -1
 
>


 
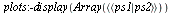> plots:-display(Array(`<,>`(`<|>`(ps1, ps2))))
 

Plot_2d Plot_2d

 
> p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
p2 := plots:-listplot([seq([`/`(`*`(i), `*`(samplingRate)), filteredSpeech[i]], i = 1 .. numelems(originalSpeech))], thickness = 0, gridlines, axes = boxed, color = black, title =
 
> plots:-display(Array(`<,>`(`<|>`(p1, p2))), view = [0 .. duration, -1 .. 1])
 

Plot_2d Plot_2d


Fly Through Animations - Learn More