| New Features in Maple 15: Magma Package |
|
 |
The Magma package provides facilities for computing with small finite magmas (sets with a single binary operation). Magmas are represented by their Cayley tables.
Enumerate small magmas
With the Magma package you can enumrate small magmas satisfying any combination of built-in properties, as well as properties that you define yourself.
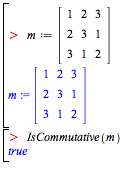
For example, build a list of the three-element commutative and associative magmas.

Test a given magma for a large number of predefined basic properties
You can test a magma for different properties, such as the existence of an identity element, the existence of a zero, commutativity, associativity, and many other equational identities.
For example:
Test a given element of a magma
You can test a given element of a magma to determine if it is a (left-sided, right-sided, or two-sided) identity or zero.
For example:

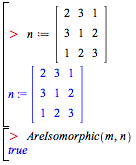
Test whether two magmas are isomorphic
The algorithm in the Magma package that tests for isomorphisms can handle magmas with thousands of elements.
For example:
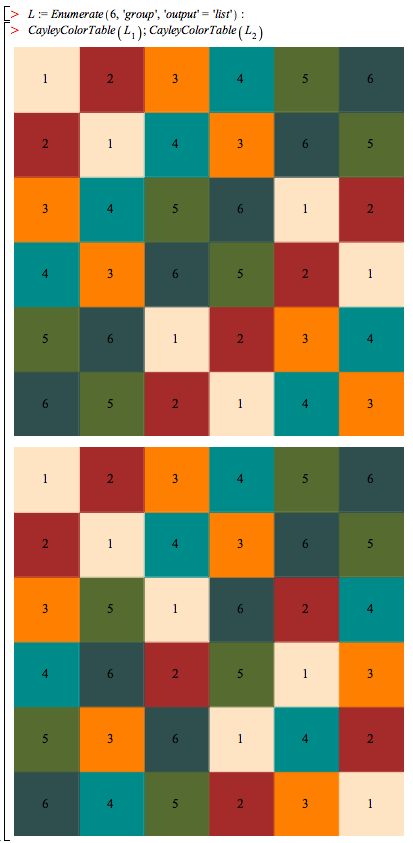
Visualize the Cayley table of a small magma
For example, compare symmetry in the Cayley tables of the commutative and non-commutative groups of order 6.
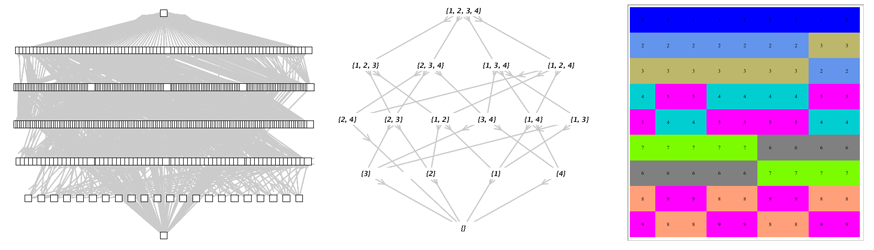
Compute distinguished subsets
The Magma package can be used to compute distinguished subsets, such as the commutant and nucleus of a magma.

And more
In addition to basic properties like commutativity, the Magma package knows about several predefined aggregate properties such as quasigroups and monoids, which are generalizations of groups, and quandles and racks, which arise as important invariants of knots.
Parallel Computing
The Magma package takes advantage of multiple cores to speed up some computations. For example:
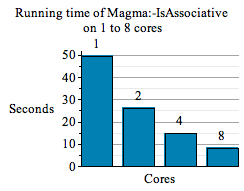
For further details, see the Magma package documentation

|

